��Ŀ����
��ͼ��ֱ���õĹ⻬ƽ�н�������MN��PQ���L����M���P����һ����ֵΪR�ĵ��裬��������� OO1O1��O�� �����������д�ֱ����ƽ�������Ϊd����ǿ�ų����Ÿ�Ӧǿ��ΪB��һ����Ϊm������Ϊr�ĵ����ab��ֱ���ڵ����ϣ���ų��ϱ߽߱����d0����ʹab���ɾ�ֹ��ʼ�ͷţ���ab���뿪�ų�ǰ�Ѿ�������ֱ���˶�����ab�뵼��ʼ�ձ������õĵ�Ӵ������������ʼ�ձ���ˮƽ��������費�ƣ�����
��1����ab���뿪�ų��±߽�ʱ���ٶȣ�
��2����ab��ͨ���ų����Ĺ����в����Ľ����ȣ�
 ��3������ab���ɾ�ֹ��ʼ�ͷŴ�Ϊ������㣬������������߶�d+d0�������ٶ�������߶�h�仯����Ӧ�ĸ��ֿ��ܵ�ͼ�ߡ�
��3������ab���ɾ�ֹ��ʼ�ͷŴ�Ϊ������㣬������������߶�d+d0�������ٶ�������߶�h�仯����Ӧ�ĸ��ֿ��ܵ�ͼ�ߡ�
��1����ab���뿪�ų��߽�ǰ�������˶����ٶ�Ϊv��
�����ĵ綯��ΪE = BLv 1��
��·�е��� I = ![]() 1��
1��
��ab������ƽ�������� mg��BIL = 0 1��
��� v = ![]() 2��
2��
(2) �������غ㶨�ɣ�mg(d0 + d) = E�� + ![]() mv2 1��
mv2 1��
��� ![]() 2��
2��
![]() 2��
2��
��3�������������d0�߶���ʱΪt0����d0 = ![]() gt02����t0 =
gt02����t0 = ![]()
���ڴų�������ʱ�ٶ�Ϊv = ![]() ����
����![]()
1 ��t0=t����d0 = ![]() ʱ��������ų���������ֱ����
ʱ��������ų���������ֱ����
 2 ��t0 < t����d0 <
2 ��t0 < t����d0 <![]() ʱ��������ų������ȼ��ٺ�����ֱ���˶�
ʱ��������ų������ȼ��ٺ�����ֱ���˶�
3 ��t0��t����d0��![]() ʱ��������ų������ȼ��ٺ�����ֱ���˶�
ʱ��������ų������ȼ��ٺ�����ֱ���˶�

 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
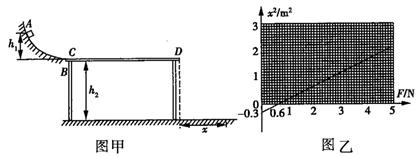
ѧϰʵ����ϵ�д� ��2012?�Ͼ���ģ����ͼa��ʾ��ˮƽ�������˹̶�һ����ֱ���õĹ⻬Բ�������Բ���������ˮƽ��������C�㣬����CD��L=1m����h2=0.5m��������Ϊm��mΪĩ֪����С����Բ����A���ɾ�ֹ�ͷţ�A�������ĸ߶�h1=0.2m��С��龭��Բ������˻�������CD�ϣ�������CD���˶�ʱʼ���ܵ�һ��ˮƽ���ҵĺ���F���ã�Ȼ���D��ɳ���ƽ���˶�������䵽ˮƽ�����ϣ���С����D����䵽��ˮƽ�����ϵ�ˮƽ����Ϊx����ͼb��x2-F��ͼ��ȡ�������ٶ�g=10m/s2��
��2012?�Ͼ���ģ����ͼa��ʾ��ˮƽ�������˹̶�һ����ֱ���õĹ⻬Բ�������Բ���������ˮƽ��������C�㣬����CD��L=1m����h2=0.5m��������Ϊm��mΪĩ֪����С����Բ����A���ɾ�ֹ�ͷţ�A�������ĸ߶�h1=0.2m��С��龭��Բ������˻�������CD�ϣ�������CD���˶�ʱʼ���ܵ�һ��ˮƽ���ҵĺ���F���ã�Ȼ���D��ɳ���ƽ���˶�������䵽ˮƽ�����ϣ���С����D����䵽��ˮƽ�����ϵ�ˮƽ����Ϊx����ͼb��x2-F��ͼ��ȡ�������ٶ�g=10m/s2�� ��ͼ��ʾ��ˮƽ��������һ�ᵯ�ɣ���˹̶���A�㣬��Ȼ״̬ʱ���Ҷ�λ��B�㣮ˮƽ�����Ҳ���һ��ֱ���õĹ⻬���MNP������״Ϊ�뾶R=0.8m��Բ����ȥ�����Ͻ�135���Բ����MNΪ����ֱֱ����P�㵽�������ֱ����Ҳ��R��������Ϊm=0.1kg����齫���ɻ���ѹ����C���ͷţ����ͨ��B�����λ����ʱ��Ĺ�ϵΪx=6t-2t2���������������P������������Բ�����g=10m/s2����
��ͼ��ʾ��ˮƽ��������һ�ᵯ�ɣ���˹̶���A�㣬��Ȼ״̬ʱ���Ҷ�λ��B�㣮ˮƽ�����Ҳ���һ��ֱ���õĹ⻬���MNP������״Ϊ�뾶R=0.8m��Բ����ȥ�����Ͻ�135���Բ����MNΪ����ֱֱ����P�㵽�������ֱ����Ҳ��R��������Ϊm=0.1kg����齫���ɻ���ѹ����C���ͷţ����ͨ��B�����λ����ʱ��Ĺ�ϵΪx=6t-2t2���������������P������������Բ�����g=10m/s2���� ��ͼ��ʾ����Դ����ֱ���õĹ⻬����������һ������������ڵ������棬Ϊʹ�����������������ڵ������ڿռ��ڼӴų�����˴ų��ķ�������ǣ�������
��ͼ��ʾ����Դ����ֱ���õĹ⻬����������һ������������ڵ������棬Ϊʹ�����������������ڵ������ڿռ��ڼӴų�����˴ų��ķ�������ǣ������� ��ֱ���õĹ⻬U�ε����0.5m�����費�ƣ����ںܴ�ĴŸ�Ӧǿ����1T����ǿ�ų��У��ų���ֱ�ڵ���ƽ�������ͼ��ʾ������Ϊ10g������Ϊ1���Ľ�����PQ���ٶ��ͷź����⻬�����»���ʼ���ܴ���ˮƽλ�ã�����ȡg=10m/s2���ʣ�
��ֱ���õĹ⻬U�ε����0.5m�����費�ƣ����ںܴ�ĴŸ�Ӧǿ����1T����ǿ�ų��У��ų���ֱ�ڵ���ƽ�������ͼ��ʾ������Ϊ10g������Ϊ1���Ľ�����PQ���ٶ��ͷź����⻬�����»���ʼ���ܴ���ˮƽλ�ã�����ȡg=10m/s2���ʣ�