题目内容
 如图所示,质量均为m的两个小球固定在长度为l的轻杆两端,直立在相互垂直的光滑墙壁和地板交界处.突然发生微小的扰动使杆无初速倒下,求当杆与竖直方向成角α时,A球对墙的作用力.
如图所示,质量均为m的两个小球固定在长度为l的轻杆两端,直立在相互垂直的光滑墙壁和地板交界处.突然发生微小的扰动使杆无初速倒下,求当杆与竖直方向成角α时,A球对墙的作用力.分析:当杆与竖直方向成角α时,根据机械能守恒定律,结合圆周运动的知识及几何关系,即可求出B球的速度;
对于B球,根据受力分析与牛顿第二定律,结合向心力公式即可求出杆对球的作用力,再根据牛顿第三定律求解A球对墙的作用力.
对于B球,根据受力分析与牛顿第二定律,结合向心力公式即可求出杆对球的作用力,再根据牛顿第三定律求解A球对墙的作用力.
解答: 解:如图所示,开始杆以A球为中心,杆长l为半径的圆周运动,对于小球B,有:
解:如图所示,开始杆以A球为中心,杆长l为半径的圆周运动,对于小球B,有:
mgcosα-N=m
根据机械能守恒定律得:
mv2=mgl(1-cosα)
由以上二式可得:N=mg(3cosα-2)
当3cosα>2,N>0,说明A球此时没有离开墙.则N1=N′sinα=mg(3cosα-2)sinα
当3cosα=2时,N=0.
所以杆对墙的作用力为N1=
答:当杆与竖直方向成角α时,A球对墙的作用力为N1为
.
 解:如图所示,开始杆以A球为中心,杆长l为半径的圆周运动,对于小球B,有:
解:如图所示,开始杆以A球为中心,杆长l为半径的圆周运动,对于小球B,有:mgcosα-N=m
| v2 |
| l |
根据机械能守恒定律得:
| 1 |
| 2 |
由以上二式可得:N=mg(3cosα-2)
当3cosα>2,N>0,说明A球此时没有离开墙.则N1=N′sinα=mg(3cosα-2)sinα
当3cosα=2时,N=0.
所以杆对墙的作用力为N1=
|
答:当杆与竖直方向成角α时,A球对墙的作用力为N1为
|
点评:此题考查机械能守恒定律与牛顿第二定律的应用,注意机械能守恒的判定,掌握几何关系的运用.同时强调作用力与反作用力的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?河西区二模)如图所示,质量均为m的A、B两球之间系着一根不计质量的弹簧,放在光滑的水平面上,A球紧靠竖直墙壁,今用水平力F将B球向左推压弹簧,平衡后,突然将F撤去,在这瞬间( )
(2011?河西区二模)如图所示,质量均为m的A、B两球之间系着一根不计质量的弹簧,放在光滑的水平面上,A球紧靠竖直墙壁,今用水平力F将B球向左推压弹簧,平衡后,突然将F撤去,在这瞬间( ) 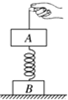 如图所示,质量均为m的物体A、B通过一个劲度系数k的轻弹簧相连,开始时B放在地面上,A、B均处于静止状态,现通过细绳将A缓慢地向上拉起,当B刚要离开地面时,求A上升距离(假设弹簧一直在弹性限度内,重力加速度g已知)
如图所示,质量均为m的物体A、B通过一个劲度系数k的轻弹簧相连,开始时B放在地面上,A、B均处于静止状态,现通过细绳将A缓慢地向上拉起,当B刚要离开地面时,求A上升距离(假设弹簧一直在弹性限度内,重力加速度g已知)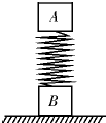 (2013?湖南模拟)如图所示,质量均为m的A、B两物体分别固定在质量不计的轻弹簧的两端,当A静止时弹簧的压缩量为l.现用一竖直向下的恒力F=3mg作用于A上,当A运动一段距离x,后撤去F,结果B刚好不离开水平面,则l:x的值为( )
(2013?湖南模拟)如图所示,质量均为m的A、B两物体分别固定在质量不计的轻弹簧的两端,当A静止时弹簧的压缩量为l.现用一竖直向下的恒力F=3mg作用于A上,当A运动一段距离x,后撤去F,结果B刚好不离开水平面,则l:x的值为( )