题目内容
如图所示，在xoy坐标平面的第一象限内有一沿y轴负方向的匀强电场，在第四象限内有一垂直于平面向里的匀强磁场，现有一质量为m、电量为+q的粒子（重力不计）从坐标原点O射入磁场，其入射方向与y的方向成45°角。当粒子运动到电场中坐标为（3L，L）的P点处时速度大小为v0,方向与x轴正方向相同。求：
(1)粒子子从O点射入磁场时的速度v；
⑵匀强电场的场强E0和匀强磁场的磁感应强度B0.
⑶在满足第(2)条件的情况下求粒子从O点运动到P点所用的时间。
解：粒子在电场中到达最高点P，则其运动轨迹如图所示。（2分）
（1）设粒子在O点时的速度大小为v，OQ段为圆周，QP段为抛物线。根据对称性可知，粒子在Q点时的速度大小也为v，方向与x轴正方向成45°角，可得： V0=vcos45° (2分)
解得：v=
v0 (1分)
（2）在粒子从Q运动到P的过程中，由动能定理得：
-qE0L=
mv02-mv2 (2分)解得：E0=
（1分）
又在匀强电场由Q到P的过程中，
水平方向的位移为
（1分）竖直方向的位移为
（1分）
可得XQP=2L，OQ=L（2分）
由OQ=2RCOS45°故粒子在OQ段圆周运动的半径：R=
L 及
得
。（2分）
（3）在Q点时，vy=v0tan45°=v0 (1分)
设粒子从Q到P所用时间为t1,在竖直方向上有：t1=
=
(1分)
粒子从O点运动到Q所用的时间为：t2=
(1分)
则粒子从O点运动到P点所用的时间为：t总=t1+t2=+=
（1分）
练习册系列答案
教材全解字词句篇系列答案
相关题目
如图所示，在竖直平面的xOy坐标系中，Oy竖直向上，Ox水平．设平面内存在沿x轴正方向的恒定风力．一物体从坐标原点沿Oy方向竖直向上抛出，初速度为v0=4m/s，不计空气阻力，到达最高点的位置如图中M点所示，（坐标格为正方形，g=10m/s2）
如图所示，在竖直平面的xoy坐标系中，oy竖直向上，ox水平．该平面内存在沿x轴正方向的恒定风力．一物体从坐标原点沿oy方向竖直向上抛出，初速度为V0=4m/s，不计空气阻力，到达最高点的位置如图中M点所示，（坐标格为正方形）求：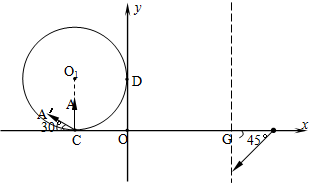
D点进入电场，最后从G点以与x轴正向夹角为45°的方向射出电场．求：
