题目内容
 如图所示,间距l=0.4m的光滑平行金属导轨与水平面夹角θ=30°,正方形区域abcd内匀强磁场的磁感应强度B=0.2T,方向垂直于斜面.甲乙两金属杆电阻R相同、质量均为m=0.02kg,垂直于导轨放置.起初,甲金属杆处在磁场的上边界ab上,乙在甲上方距甲也为l处.现将两金属杆同时由静止释放,并同时在甲金属杆上施加一个沿着导轨的拉力F,使甲金属杆始终以a=5m/s2的加速度沿导轨匀加速运动,已知乙金属杆刚进入磁场时做匀速运动,取g=10m/s2,则( )
如图所示,间距l=0.4m的光滑平行金属导轨与水平面夹角θ=30°,正方形区域abcd内匀强磁场的磁感应强度B=0.2T,方向垂直于斜面.甲乙两金属杆电阻R相同、质量均为m=0.02kg,垂直于导轨放置.起初,甲金属杆处在磁场的上边界ab上,乙在甲上方距甲也为l处.现将两金属杆同时由静止释放,并同时在甲金属杆上施加一个沿着导轨的拉力F,使甲金属杆始终以a=5m/s2的加速度沿导轨匀加速运动,已知乙金属杆刚进入磁场时做匀速运动,取g=10m/s2,则( )分析:解答本题应抓住:
1、乙金属杆进入磁场前,沿斜面向下的加速度跟甲的加速度相同,甲乙均做加速运动;由运动学公式求出乙进入磁场时的速度,乙金属杆刚进入磁场时做匀速运动,根据平衡条件和安培力公式求解R;
2、甲乙运动时间相等,由运动学公式求出甲金属杆在磁场中运动的时间;
3、甲在磁场中做匀加速运动时,根据牛顿第二定律得知,外力F始终等于安培力,由P=Fv分析功率的变化;
4、乙金属杆在磁场中匀速运动过程中,安培力的功率等于电路中电阻的热功率.
1、乙金属杆进入磁场前,沿斜面向下的加速度跟甲的加速度相同,甲乙均做加速运动;由运动学公式求出乙进入磁场时的速度,乙金属杆刚进入磁场时做匀速运动,根据平衡条件和安培力公式求解R;
2、甲乙运动时间相等,由运动学公式求出甲金属杆在磁场中运动的时间;
3、甲在磁场中做匀加速运动时,根据牛顿第二定律得知,外力F始终等于安培力,由P=Fv分析功率的变化;
4、乙金属杆在磁场中匀速运动过程中,安培力的功率等于电路中电阻的热功率.
解答:解:A、乙金属杆进入磁场前的加速度为a=gsin30°=5m/s2,可见其加速度与甲的加速度相同,甲乙均做相同的加速运动.当乙进入磁场时,甲刚出磁场.
乙进入磁场时:v=
=2m/s,由于已知乙金属杆刚进入磁场时做匀速运动,受力平衡有:
mgsinθ=
=
故求得:R=
,代入数据的R=0.064Ω,故A错误.
B、甲在磁场中做匀加速运动,由l=
at2,可得甲金属杆在磁场中运动的时间是0.4s,故B正确.
C、甲在磁场中做匀加速运动时,根据牛顿第二定律得:F+mgsin30°-FA=ma,得:F=FA,即外力F始终等于安培力,由于速度一直增加,安培力一直增大,F一直增大,其功率也增大,故C正确.
D、乙金属杆进入磁场时做匀速运动,由功能关系知:乙金属杆在磁场中运动过程中安培力的功率等于电路中电阻的热功率,即P=I22R=(
)22R,v=
,解得P=0.2W,故D错误.
故选BC
乙进入磁场时:v=
| 2glsinθ |
mgsinθ=
| B2l2v |
| 2R |
B2l2
| ||
| 2R |
故求得:R=
B2l2
| ||
| 2mgsinθ |
B、甲在磁场中做匀加速运动,由l=
| 1 |
| 2 |
C、甲在磁场中做匀加速运动时,根据牛顿第二定律得:F+mgsin30°-FA=ma,得:F=FA,即外力F始终等于安培力,由于速度一直增加,安培力一直增大,F一直增大,其功率也增大,故C正确.
D、乙金属杆进入磁场时做匀速运动,由功能关系知:乙金属杆在磁场中运动过程中安培力的功率等于电路中电阻的热功率,即P=I22R=(
| Blv |
| 2R |
| 2glsinθ |
故选BC
点评:本题关键要抓住乙金属杆进入磁场前,两棒的加速度相同,运动情况相同,再根据牛顿第二定律、运动学公式和功能关系求解.

练习册系列答案
相关题目
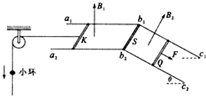 (2011?四川)如图所示,间距l=0.3m的平行金属导轨a1b1c1和a2b2c2分别固定在两个竖直面内,在水平面a1b1b2a2区域内和倾角θ=37°的斜面c1b1b2c2区域内分别有磁感应强度B1=0.4T、方向竖直向上和B2=1T、方向垂直于斜面向上的匀强磁场.电阻R=0.3Ω、质量m1=0.1kg、长为l的相同导体杆K、S、Q分别放置在导轨上,S杆的两端固定在b1、b2点,K、Q杆可沿导轨无摩擦滑动且始终接触良好.一端系于K杆中点的轻绳平行于导轨绕过轻质滑轮自然下垂,绳上穿有质量m2=0.05kg的小环.已知小环以a=6m/s2的加速度沿绳下滑,K杆保持静止,Q杆在垂直于杆且沿斜面向下的拉力F作用下匀速运动.不计导轨电阻和滑轮摩擦,绳不可伸长.取g=10m/s2,sin37°=0.6,cos37°=0.8.求
(2011?四川)如图所示,间距l=0.3m的平行金属导轨a1b1c1和a2b2c2分别固定在两个竖直面内,在水平面a1b1b2a2区域内和倾角θ=37°的斜面c1b1b2c2区域内分别有磁感应强度B1=0.4T、方向竖直向上和B2=1T、方向垂直于斜面向上的匀强磁场.电阻R=0.3Ω、质量m1=0.1kg、长为l的相同导体杆K、S、Q分别放置在导轨上,S杆的两端固定在b1、b2点,K、Q杆可沿导轨无摩擦滑动且始终接触良好.一端系于K杆中点的轻绳平行于导轨绕过轻质滑轮自然下垂,绳上穿有质量m2=0.05kg的小环.已知小环以a=6m/s2的加速度沿绳下滑,K杆保持静止,Q杆在垂直于杆且沿斜面向下的拉力F作用下匀速运动.不计导轨电阻和滑轮摩擦,绳不可伸长.取g=10m/s2,sin37°=0.6,cos37°=0.8.求
 =
= 的斜面c1b1b2c2区域内分别有磁感应强度B1=0.4T、方向竖直向上和B2=1T、方向垂直于斜面向上的匀强磁场。电阻R=0.3
的斜面c1b1b2c2区域内分别有磁感应强度B1=0.4T、方向竖直向上和B2=1T、方向垂直于斜面向上的匀强磁场。电阻R=0.3 、质量m1=0.1kg、长为
、质量m1=0.1kg、长为 的相同导体杆K、S、Q分别放置在导轨上,S杆的两端固定在b1、b2点,K、Q杆可沿导轨无摩擦滑动且始终接触良好。一端系于K杆中点的轻绳平行于导轨绕过轻质滑轮自然下垂,绳上穿有质量m2=0.05kg的小环。已知小环以a=6 m/s2的加速度沿绳下滑,K杆保持静止,Q杆在垂直于杆且沿斜面向下的拉力F作用下匀速运动。不计导轨电阻和滑轮摩擦,绳不可伸长。取g=10 m/s2,sin
的相同导体杆K、S、Q分别放置在导轨上,S杆的两端固定在b1、b2点,K、Q杆可沿导轨无摩擦滑动且始终接触良好。一端系于K杆中点的轻绳平行于导轨绕过轻质滑轮自然下垂,绳上穿有质量m2=0.05kg的小环。已知小环以a=6 m/s2的加速度沿绳下滑,K杆保持静止,Q杆在垂直于杆且沿斜面向下的拉力F作用下匀速运动。不计导轨电阻和滑轮摩擦,绳不可伸长。取g=10 m/s2,sin
