题目内容
2. 如图所示,靠摩擦传动做匀速转动的大、小两轮接触面互不打滑,大轮半径是小轮半径的2倍.A、B分别为大、小轮边缘上的点,C为大轮上一条半径的中点.则( )
如图所示,靠摩擦传动做匀速转动的大、小两轮接触面互不打滑,大轮半径是小轮半径的2倍.A、B分别为大、小轮边缘上的点,C为大轮上一条半径的中点.则( )| A. | 两轮的边沿转动的线速度大小相等 | B. | 大轮转动的角速度是小轮的2倍 | ||
| C. | 质点加速度aA=2aB | D. | 质点加速度aB=4aC |
分析 在转盘问题中要明确转盘接触的边缘线速度大小相同,同一转盘上角速度相同,然后利用角速度、线速度、半径之间的关系以及向心加速度公式进行求解.
解答 解:A、两轮接触面互不打滑,则两轮的边沿转动的线速度大小相等,故A正确.
B、由v=ωr、vA=vB、rA=2rB得ωB=2ωA,即小轮的角速度是大轮的2倍,故B错误.
C、对于A、B,因为vA=vB、rA=2rB,由a=$\frac{{v}^{2}}{r}$得aB=2aA.故C错误.
D、根据转盘转动特点可知:ωA=ωC
故得aB=2aC.
对于B、C,rB=rC,由a=ω2r得aB=4aC.故D正确.
故选:AD.
点评 解决本题的关键掌握靠摩擦传动两个轮子边缘上的各点具有相同的线速度,共轴转动的点,具有相同的角速度,灵活选择公式,由比例法解答.

练习册系列答案
相关题目
12.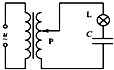 如图所示,理想变压器原线圈接有交流电源,当副线圈上的滑片P处于图示位置时,灯泡L能发光. 要使灯泡变亮,可以采取的方法有( )
如图所示,理想变压器原线圈接有交流电源,当副线圈上的滑片P处于图示位置时,灯泡L能发光. 要使灯泡变亮,可以采取的方法有( )
 如图所示,理想变压器原线圈接有交流电源,当副线圈上的滑片P处于图示位置时,灯泡L能发光. 要使灯泡变亮,可以采取的方法有( )
如图所示,理想变压器原线圈接有交流电源,当副线圈上的滑片P处于图示位置时,灯泡L能发光. 要使灯泡变亮,可以采取的方法有( )| A. | 向下滑动P | B. | 减小电容器C的电容 | ||
| C. | 减小交流电源的频率 | D. | 增大交流电源的电压 |
10.关于曲线运动的叙谜,正确的是( )
| A. | 做曲线运动的物体,速度方向时刻变化,故曲线运动一定是变加速运动 | |
| B. | 变速运动一定是曲线运动 | |
| C. | 所有曲线运动都一定是变速运动 | |
| D. | 物体只有受到方向时刻变化的力的作用才可能做曲线运动 |
17.关于曲线运动,下列说法正确的是( )
| A. | 做曲线运动物体的速度方向可以不变 | |
| B. | 曲线运动一定是变速运动 | |
| C. | 物体受到变力作用时就做曲线运动 | |
| D. | 物体做圆周运动,所受的合力一定指向圆心 |
7.(多选)关于曲线运动,下列说法中正确的是( )
| A. | 曲线运动一定是变速运动 | B. | 变速运动一定是曲线运动 | ||
| C. | 曲线运动可能是匀变速运动 | D. | 变加速运动一定是曲线运动 |
14.关于运动的合成,下列说法正确的是( )
| A. | 两个匀速直线运动的合运动一定是匀速直线运动 | |
| B. | 一个匀速直线运动和一个匀加速直线运动的合运动一定是曲线运动 | |
| C. | 两个加速度不等的匀加速直线运动的合运动可能是匀变速曲线运动 | |
| D. | 两个加速度不等的匀加速直线运动的合运动不可能是匀变速直线运动 |
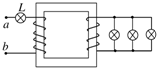 如图所示,在一理想变压器的初、次级线圈接有4个相同的灯泡,若4个灯泡都正常发光,则该变压器初、次级线圈的匝数比n1:n2等于( )
如图所示,在一理想变压器的初、次级线圈接有4个相同的灯泡,若4个灯泡都正常发光,则该变压器初、次级线圈的匝数比n1:n2等于( )
 一列简谐横波沿x轴正方向传播,t=0时刻波形如图所示,振幅5cm,从图示时刻起经0.5s时间x=2的质点P刚好第二次出现波峰,求:
一列简谐横波沿x轴正方向传播,t=0时刻波形如图所示,振幅5cm,从图示时刻起经0.5s时间x=2的质点P刚好第二次出现波峰,求: