题目内容
如图，在竖直向下，场强为E的匀强电场中，长为l的绝缘轻杆可绕固定轴O在竖直面内无摩擦转动，两个小球A、B固定于杆的两端，A、B的质量分别为m1和m2（m1＜m2），A带负电，电量为q1，B带正电，电量为q2．杆从静止开始由水平位置转到竖直位置，在此过程中电场力做功 ，在竖直位置处两球的总动能 ．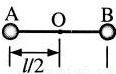
【答案】分析：首先跟据所受电场力情况，判断出杆是顺时针还是逆时针转动，然后根据电场力做功特点分别求出电场力对A、B两球所做功，根据动能定理求两球的动能．
解答：解：因为杆及AB受力的合力矩为顺时针，所以系统沿顺时针转动到竖直位置，电场力对A和B都做正功，电场力对A、B做总功为：
．
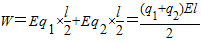在此过程中重力对A做正功，对B做负功，设两球总动能为Ek，由用动能定理得：
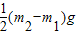l+
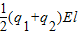=Ek-0
所以两球总动能为：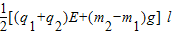
故答案为：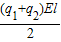
，
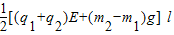
点评：本题考查力矩及电场力的功和重力的功；难点是判断系统转动方向，从而确定电场力、重力做功情况．
解答：解：因为杆及AB受力的合力矩为顺时针，所以系统沿顺时针转动到竖直位置，电场力对A和B都做正功，电场力对A、B做总功为：
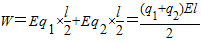．在此过程中重力对A做正功，对B做负功，设两球总动能为Ek，由用动能定理得：
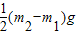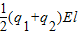l+=Ek-0所以两球总动能为：
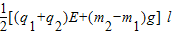
故答案为：
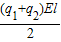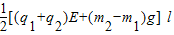
，点评：本题考查力矩及电场力的功和重力的功；难点是判断系统转动方向，从而确定电场力、重力做功情况．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，竖直平面内有一边长为L、质量为m，电阻为R的正方形线框在竖直向下的匀强重力场和水平方向的磁场组成的复合场以初速度v0水平抛出．磁场方向与线框平面垂直，磁场的磁感应强度随竖直向下的z轴按B=B0+kz的规律均匀增大．已知重力加速度为g．求：
如图所示，在竖直向下的匀强电场中有一绝缘的光滑轨道，一个带负电的小球从斜轨上的A点由静止释放，沿轨道滑下，已知小球的质量为m，电荷量为-q，匀强电场的场擞大小为E，斜轨道的倾角为a，圆轨迹道半径为R，小球的重力大于受的电场力．
