题目内容
【题目】竖直面内一倾斜轨道与一足够长的水平轨道通过一小段光滑圆弧平滑连接，小物块B静止于水平轨道的最左端，如图（a）所示。t=0时刻，小物块A在倾斜轨道上从静止开始下滑，一段时间后与B发生弹性碰撞（碰撞时间极短）；当A返回到倾斜轨道上的P点（图中未标出）时，速度减为0，此时对其施加一外力，使其在倾斜轨道上保持静止。物块A运动的v-t图像如图（b）所示，图中的v1和t1均为未知量。已知A的质量为m，初始时A与B的高度差为H，重力加速度大小为g，不计空气阻力。
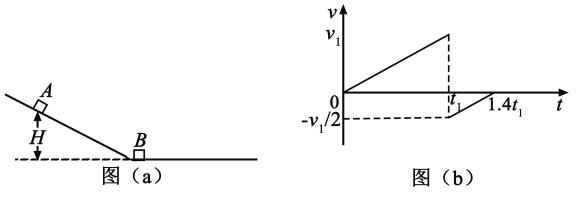
（1）求物块B的质量；
（2）在图（b）所描述的整个运动过程中，求物块A克服摩擦力所做的功；
（3）已知两物块与轨道间的动摩擦因数均相等，在物块B停止运动后，改变物块与轨道间的动摩擦因数，然后将A从P点释放，一段时间后A刚好能与B再次碰上。求改变前面动摩擦因数的比值。
【答案】（1）3m （2）
（3）
【解析】
（1）物块A和物块B发生碰撞后一瞬间的速度分别为
、
，弹性碰撞瞬间，动量守恒，机械能守恒，即：
联立方程解得：
；
根据v-t图象可知，
解得：
（2）设斜面的倾角为
，根据牛顿第二定律得
当物块A沿斜面下滑时：
，由v-t图象知：
当物体A沿斜面上滑时：
，由v-t图象知：
解得：
；
又因下滑位移
则碰后A反弹，沿斜面上滑的最大位移为：
其中
为P点离水平面得高度，即
解得
故在图（b）描述的整个过程中，物块A克服摩擦力做的总功为：
（3）设物块B在水平面上最远的滑行距离为
，设原来的摩擦因为为
则以A和B组成的系统，根据能量守恒定律有：
设改变后的摩擦因数为
，然后将A从P点释放，A恰好能与B再次碰上，即A恰好滑到物块B位置时，速度减为零，以A为研究对象，根据能量守恒定律得：
又据（2）的结论可知：
，得：
联立解得，改变前与改变后的摩擦因素之比为：
。
