题目内容
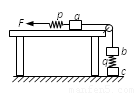
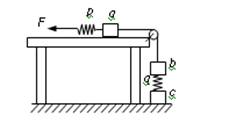
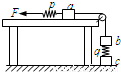
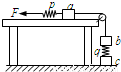
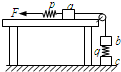三个重量均为10N的相同木块a、b、c和两个劲度均为500N/m的相同轻弹簧p、q用细线连接如图，其中a放在光滑水平桌面上．开始时p弹簧处于原长，木块都处于静止．现用水平力缓慢地向左拉p弹簧的左端，直到c木块刚好离开水平地面为止．该过程p弹簧的左端向左移动的距离是（轻弹簧和细线的重量都忽略不计）（ ）分析：刚开始弹簧p处于原长，而弹簧q被压缩；之后p、q弹簧都伸长；细线的形变量忽略不计，故可以结合胡克定律和几何关系得到p弹簧的左端向左移动的距离．
解答：解：刚开始弹簧p处于原长，而弹簧q被压缩，设压缩量为x1，根据胡克定律，有
mg=kx1
解得
x1=
=
=0.02m
用水平力缓慢地向左拉p弹簧的左端，直到c木块刚好离开水平地面为止，此时，对物体C受力分析，受重力和拉力，设弹簧伸长量为x2，根据胡克定律，有
mg=kx2
解得
x2=
=
=0.02m
对物体b受力分析，受重力mg、弹簧拉力F和细线拉力T，根据平衡条件，有
T=F+mg=20N
对物体a受力分析，受重力、支持力、细线拉力T和弹簧弹力F′，根据平衡条件，有
F′=T=20N
设弹簧p伸长量为x3，根据胡克定律，有
F′=kx3
解得
x3=
=
=0.04m
根据几何关系，p弹簧的左端向左移动的距离是：x=x1+x2+x3=0.08m
故p弹簧的左端向左移动的距离是0.08m，即8cm．
故选C．
mg=kx1
解得
x1=
| mg |
| k |
| 10N |
| 500N/m |
用水平力缓慢地向左拉p弹簧的左端，直到c木块刚好离开水平地面为止，此时，对物体C受力分析，受重力和拉力，设弹簧伸长量为x2，根据胡克定律，有
mg=kx2
解得
x2=
| mg |
| k |
| 10N |
| 500N/m |
对物体b受力分析，受重力mg、弹簧拉力F和细线拉力T，根据平衡条件，有
T=F+mg=20N
对物体a受力分析，受重力、支持力、细线拉力T和弹簧弹力F′，根据平衡条件，有
F′=T=20N
设弹簧p伸长量为x3，根据胡克定律，有
F′=kx3
解得
x3=
| F′ |
| k |
| 20N |
| 500N/m |
根据几何关系，p弹簧的左端向左移动的距离是：x=x1+x2+x3=0.08m
故p弹簧的左端向左移动的距离是0.08m，即8cm．
故选C．
点评：本题关键是找出临界状态，然后求出弹簧各个时刻的压缩量和伸长量，最后根据几何关系得到p弹簧的左端向左移动的距离．
练习册系列答案
相关题目
