题目内容
(10分)如图所示，半径为R的
光滑圆弧轨道竖直放置，底端与光滑的水平轨道相接，质量为m的小球B静止光滑水平轨道上，其左侧连接了一轻质弹簧，质量为m的小球A自圆弧轨道的顶端由静止释放，重力加速度为g，小球可视为质点．
求：（1）小球A滑到圆弧面底端时的速度大小．
（2）小球A撞击轻质弹簧的过程中，弹簧的最大弹性势能为多少．
【答案】
（1）
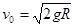（2）
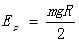
【解析】
试题分析：（1）设A球到达圆弧底端时的速度为v0，由机械能守恒定律有：
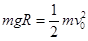①（2分）
A球到达圆弧底端时的速度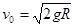 ②（2分）
（2）当A、B两球速度相同时，弹簧的弹性势能最大，设共同速度为v（1分）
由动量守恒定律有：
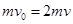③（2分）
得
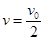④（1分）
由能量守恒可知，弹簧的最大弹性势能
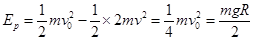⑤（2分）
考点：机械能守恒定律 动量守恒定律
练习册系列答案
相关题目
冲上圆弧轨道，已知圆弧轨道的质量M=3m，不计摩擦和空气阻力，
，电动机M的内电阻为
，当开关s闭合，电动机转动稳定后，理想电压表的读数为
。若电动机除了内电阻外不计其他损耗。求:（1）电动机输出的机械功率P1.（2）电路消耗的总功率P。