Question

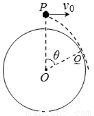
如图所示，在水平放置的半径为R的圆柱体轴线的正上方的P点，将一个小球以水平速度v0垂直圆柱体的轴线抛出，小球飞行一段时间后恰好从圆柱体的Q点沿切线飞过，测得O、Q连线与竖直方向的夹角为θ，那么小球完成这段飞行的时间是

A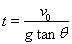．???????? B．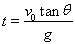

C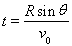．????????? D．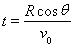

 

Answer 1

【答案】

BC

【解析】

试题分析：小球以水平速度v0垂直圆柱体的轴线抛出后做平抛运动，将其沿水平和竖直方向分解，在水平方向上做匀速直线运动，在竖直方向上做自由落体运动。设小球到达Q点时的速度，竖直速度为，则由题设及几何知识得，小球从P到Q在水平方向上发生的位移为，速度的方向与水平方向的夹角为θ，于是，根据运动规律得：，，联立以上各式解得：，或，故选BC。

考点：本题考查平抛运动和运动的分解知识，意在考查考生对平抛运动规律的掌握情况和综合解决问题的能力。