题目内容
2. 如图所示,在直角坐标系xOy的第二象限存在沿y轴正方向的匀强电场,电场强度的大小为E1,在y轴的左侧存在垂直纸面的匀强磁场,现有一质量为m,带电荷量为+q的带电粒子从第二象限的A点(-3L,L)以初速度v0沿x轴正方向射入后刚好做匀速直线运动,不计带电粒子的重力.
如图所示,在直角坐标系xOy的第二象限存在沿y轴正方向的匀强电场,电场强度的大小为E1,在y轴的左侧存在垂直纸面的匀强磁场,现有一质量为m,带电荷量为+q的带电粒子从第二象限的A点(-3L,L)以初速度v0沿x轴正方向射入后刚好做匀速直线运动,不计带电粒子的重力.(1)求匀强磁场B1的大小和方向;
(2)撤去第二象限的匀强电场,同时调节磁感应强度的大小为B2,使带电粒子刚好从B点(-L,0)进入第三象限,求磁感应强度B2的大小及带电粒子从A点运动到B点所用的时间.
分析 (1)由粒子受力平衡得到电场力等于洛伦兹力,进而求得磁感应强度;
(2)由粒子做匀速圆周运动的轨迹,根据几何关系的到粒子运动半径,进而求得磁感应强度及中心角,从而得到运动时间.
解答 解:(1)带电粒子做匀速直线运动,其所受合力为零,由于粒子带正电荷,带电粒子受到的电场力方向沿y轴正方向,大小为qE1,所以带电粒子受到的洛伦兹力方向沿y轴负方向,根据左手定则判断磁场方向垂直纸面向里;
根据带电粒子受的洛伦兹力等于电场力,即:qv0B1=qE1,
可得:${B_1}=\frac{E_1}{v_0}$;
(2)撤去电场后,带电粒子仅受洛伦兹力作用做圆周运动,由几何关系可得:R2=(2L)2+(R-L)2,
解得:R=2.5L;
粒子转过的中心角为:$θ=arcsin\frac{2L}{R}=arcsin\frac{4}{5}=53°$;
由牛顿第二定律可得:$q{v_0}{B_2}=m\frac{v_0^2}{R}$,
解得:${B_2}=\frac{{2m{v_0}}}{5qL}$;
又有$T=\frac{2πR}{v_0}$,所以,带电粒子从A点运动到B点所用的时间为:$t=\frac{θ}{360°}T$=$\frac{53πL}{{72{v_0}}}$;
答:(1)匀强磁场B1的大小为$\frac{{E}_{1}}{{v}_{0}}$,方向垂直纸面向里;
(2)撤去第二象限的匀强电场,同时调节磁感应强度的大小为B2,使带电粒子刚好从B点(-L,0)进入第三象限,则磁感应强度B2的大小为$\frac{2m{v}_{0}}{5qL}$,带电粒子从A点运动到B点所用的时间为$\frac{53πL}{72{v}_{0}}$.
点评 带电粒子在匀强磁场中运动,一般根据几何关系求得半径、中心角,进而求得运动时间;再由牛顿第二定律求取速度、磁感应强度等相关问题.

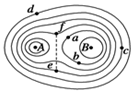 位于A、B处的两个带有不等量负电的点电荷在平面内电势分布如图所示,图中实线表示等势线,则( )
位于A、B处的两个带有不等量负电的点电荷在平面内电势分布如图所示,图中实线表示等势线,则( )| A. | a点和b点的电场强度相同 | |
| B. | c、d两点电势差大于0 | |
| C. | 负电荷从a点移到c点,电场力做负功 | |
| D. | 正电荷从e点沿图中虚线移到f点电势能先减小后增大 |
| A. | $m{g_0}{R^2}({\frac{1}{R_2}-\frac{1}{R_1}})$ | B. | $mg{R^2}({\frac{1}{R_2}-\frac{1}{R_1}})$ | ||
| C. | $\frac{{mg{R^2}}}{2}({\frac{1}{R_2}-\frac{1}{R_1}})$ | D. | $\frac{{m{g_0}{R^2}}}{2}({\frac{1}{R_2}-\frac{1}{R_1}})$ |
| A. | 卫星运动的速率减小 | B. | 卫星运动的角速度变大 | ||
| C. | 卫星运动的周期变大 | D. | 卫星的向心加速度变小 |
 自行车和汽车同时驶过平直公路上的同一地点,此后其运动的v-t图象如图所示,自行车在t=50s时追上汽车,则( )
自行车和汽车同时驶过平直公路上的同一地点,此后其运动的v-t图象如图所示,自行车在t=50s时追上汽车,则( )| A. | 汽车的位移为100 m | B. | 汽车的运动时间为20 s | ||
| C. | 汽车的加速度大小为0.25 m/s2 | D. | 汽车停止运动时,二者间距最大 |
 为研究高压输电减少电能损失的规律,设计如图所示演示实验电路.变压器T1的原线圈接入u1=14.14sin100πt(V)的学生电源,变压器T2的副线圈接入“10V,10W”的灯泡,调节各线圈匝数使灯泡正常发光,两变压器之间的输电导线总电阻r=3Ω.下列判断正确的是( )
为研究高压输电减少电能损失的规律,设计如图所示演示实验电路.变压器T1的原线圈接入u1=14.14sin100πt(V)的学生电源,变压器T2的副线圈接入“10V,10W”的灯泡,调节各线圈匝数使灯泡正常发光,两变压器之间的输电导线总电阻r=3Ω.下列判断正确的是( )| A. | 变压器T1的输出功率大于10W | |
| B. | 灯泡两端的电压为u4=12sin100πt(V) | |
| C. | 若只使T1的原线圈匝数n1减少,则输电导线消耗的电功率不变 | |
| D. | 若在灯L两端再并联一个相同的灯泡,则输电导线消耗的电功率增大 |
| A. | 当分子间的引力与斥力平衡时,分子势能最大 | |
| B. | 由熵的定义可知,熵较大的宏观状态就是无序程度很大的宏观状态,也就是出现概率较大的宏观状态 | |
| C. | 液体的饱和汽压与饱和汽的体积有关 | |
| D. | 若一定质量的理想气体被压缩且吸收热量,则压强一定增大 | |
| E. | 若一定质量的理想气体分子平均动能减小,且外界对气体做功,则气体一定放热 |
 如图所示,质点a、b在直线PQ上的两个端点,质点a从P沿PQ做初速度为0的匀加速直线运动,经过位移x1时质点b从Q沿QP方向做初速度为0的匀加速直线运动,位移x2时和质点a相遇,两质点的加速度大小相同,则PQ距离为( )
如图所示,质点a、b在直线PQ上的两个端点,质点a从P沿PQ做初速度为0的匀加速直线运动,经过位移x1时质点b从Q沿QP方向做初速度为0的匀加速直线运动,位移x2时和质点a相遇,两质点的加速度大小相同,则PQ距离为( )| A. | x1+2x2+2$\sqrt{{x}_{1}{x}_{2}}$ | B. | 2x1+x2+2$\sqrt{{x}_{1}{x}_{2}}$ | C. | x1+2x2+$\sqrt{2{x}_{1}{x}_{2}}$ | D. | 2x1+x2+$\sqrt{2{x}_{1}{x}_{2}}$ |