Question

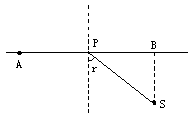
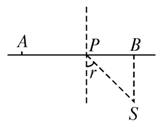
如图所示,一个人发现水中S处有一溺水者,溺水者离岸的距离SB=10 m,而发现者在A处,距B点的距离为20 m,此人在岸上跑动的速度为5 m/s,而在水中的速度为1 m/s,发现者为尽快到达溺水者处,他应在何处下水?

 

Answer 1

【答案】

2.04 m

【解析】

试题分析：这是一个运动学问题,但与光的折射现象有相似之处,发现者为了尽快到达S处,假设他从P处下水.（BP=x),就相当于入射光的入射角为i=90°,sini/sinr=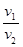=5,

因为sinr=,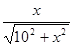

所以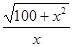=5,

解得x=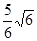m=2.04 m.

即发现者应从距B点2.04 m处下水

考点：光的传播  光的折射

点评：此题关键是画出光路图，清楚光的传播路径，根据光的折射定律解决实际问题是考查学生的应用能力。