Question

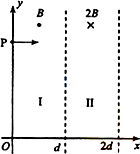
如图，在区域I(0≤x≤d)和区域II(d≤x≤2 d)内分别存在匀强磁场，磁感应强度大小都为B，但方向相反，且都垂直于Oxy平面．一质量为m，带电荷量q(q＞0)的粒子于某时刻从y轴上的P点射入区域I，其速度方向沿x轴正向．已知粒子在离开区域I时，速度方向与x轴正方向的夹角为30°；求

(1)粒子射入区域I时速度的大小；

(2)当粒子离开区域II时，出射位置与P点位置的y坐标之差．

(3)粒子从P点入射到离开区域II时所经历的时间

Answer 1

答案：
解析：

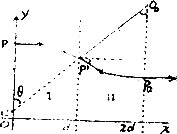
　　详解：(1)设粒子a在I内做匀速圆周运动的圆心为C(在y轴上)，半径为Ral，粒子速率为va，运动轨迹与两磁场区域边界的交点为，如图，由洛伦兹力公式和牛顿第二定律有，

　　

　　由几何关系有∠PC＝；Ra1＝

　　式中＝30°，由上面三式可得va＝

　　(2)设粒子a在Ⅱ内做圆周运动的圆心为Oa，半径为Ra2，射出点为Pa

　　Ra2＝Ra1

　　∠OaPa＝

　　由对称性知，Pa点与P的纵坐标之差为

　　Yp－yPa＝2Ra1(1－cos)＝4d－3.46d

　　(3)t1＋t2＝πm/3qB