题目内容
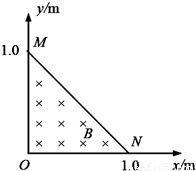 如图所示,磁感应强度为B=2.0×10-3T的磁场分布在xOy平面上的MON三角形区域,其中M、N点距坐标原点O均为1.0m,磁场方向垂直纸面向里.坐标原点O处有一个粒子源,不断地向xOy平面发射比荷为
如图所示,磁感应强度为B=2.0×10-3T的磁场分布在xOy平面上的MON三角形区域,其中M、N点距坐标原点O均为1.0m,磁场方向垂直纸面向里.坐标原点O处有一个粒子源,不断地向xOy平面发射比荷为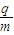 =5×107C/kg的带正电粒子,它们的速度大小都是v=5×104m/s,与x轴正方向的夹角分布在0~90°范围内.
=5×107C/kg的带正电粒子,它们的速度大小都是v=5×104m/s,与x轴正方向的夹角分布在0~90°范围内.(1)求平行于x轴射入的粒子,出射点的位置及在磁场中运动时间;
(2)若从O点入射的与x轴正方向成θ角的粒子恰好不能从MN边射出,试画出此粒子运动的轨迹;
(3)求能从直线MN射出的粒子,从粒子源O发射时的速度与x轴正向夹角范围.
(可供参考几个三角函数值sin41°=0.656,sin38°=0.616).
【答案】分析:带电粒子在磁场中受到洛伦兹力作用下做匀速圆周运动,洛伦兹力始终与速度相垂直,因此洛伦兹力不做功,所以动能不变,速度也不变.带电粒子在磁场中运动,由左手定则可判定洛伦兹力方向.从而可根据运动轨迹来确定洛伦兹力的方向,最终能得出磁感应强度大小与方向.
当平行于x轴射入的粒子时,运动轨迹对应的圆心正好落在y轴上,当已知条件算出圆弧对应的半径,可得运动轨迹恰好是圆的四分之一.从而确定出射点的位置与运动时间.
从O点入射的与x轴正方向成θ角的粒子恰好不能从MN边射出,则运动轨迹与MN直线相切,从而可确定圆弧的圆心,算出半径并画出圆弧.
由题意可知,能从直线MN射出的粒子就在前两个问题之间入射,就能射出.运用物理规律与数学知识从而求出发射时的速度与x轴正向夹角范围.
解答: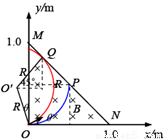 解:(1)粒子在磁场中做圆周运动,由洛伦兹力提供向心力有:qvB=m
解:(1)粒子在磁场中做圆周运动,由洛伦兹力提供向心力有:qvB=m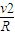
解得:R=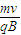
代入数据有:R=0.5m
作平行于x轴射入粒子的轨迹,由磁场的形状可知,粒子刚好在磁场中做了 圆弧,从MN中点P射出磁场,出射点的坐标P(0.5,0.5),
圆弧,从MN中点P射出磁场,出射点的坐标P(0.5,0.5),
如图所示.
粒子在磁场中运动周期T=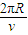
从P射出粒子在磁场中运动时间:
t=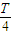 =
=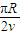 =
=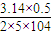 =1.57×10-5s.
=1.57×10-5s.
(2)当粒子的运动轨迹恰好与MN直线相切时,粒子恰好不能从MN边射出,粒子运动轨迹如答图1所示.其中与MN相切于Q点.
(3)Q点的x坐标:x=Rcos45°-Rsinθ
y坐标:y=Rsin45°+Rcosθ
又Q点在MN直线上,有y=1-x
代入数据,解得:cosθ-sinθ=2-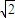
又cos2θ+sin2θ=1
联立得:sin2θ=4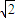 -5=0.656,
-5=0.656,
解得:θ=20.5°
所以从MN射出粒子初速方向与x轴正向夹角范围为:[0,20.5°)
点评:带电粒子在磁场中做匀速圆周运动,处理时注意:定圆心、画轨迹、求半径.
当平行于x轴射入的粒子时,运动轨迹对应的圆心正好落在y轴上,当已知条件算出圆弧对应的半径,可得运动轨迹恰好是圆的四分之一.从而确定出射点的位置与运动时间.
从O点入射的与x轴正方向成θ角的粒子恰好不能从MN边射出,则运动轨迹与MN直线相切,从而可确定圆弧的圆心,算出半径并画出圆弧.
由题意可知,能从直线MN射出的粒子就在前两个问题之间入射,就能射出.运用物理规律与数学知识从而求出发射时的速度与x轴正向夹角范围.
解答:
 解:(1)粒子在磁场中做圆周运动,由洛伦兹力提供向心力有:qvB=m
解:(1)粒子在磁场中做圆周运动,由洛伦兹力提供向心力有:qvB=m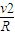
解得:R=
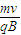
代入数据有:R=0.5m
作平行于x轴射入粒子的轨迹,由磁场的形状可知,粒子刚好在磁场中做了
 圆弧,从MN中点P射出磁场,出射点的坐标P(0.5,0.5),
圆弧,从MN中点P射出磁场,出射点的坐标P(0.5,0.5),如图所示.
粒子在磁场中运动周期T=
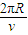
从P射出粒子在磁场中运动时间:
t=
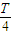 =
=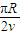 =
=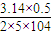 =1.57×10-5s.
=1.57×10-5s.(2)当粒子的运动轨迹恰好与MN直线相切时,粒子恰好不能从MN边射出,粒子运动轨迹如答图1所示.其中与MN相切于Q点.
(3)Q点的x坐标:x=Rcos45°-Rsinθ
y坐标:y=Rsin45°+Rcosθ
又Q点在MN直线上,有y=1-x
代入数据,解得:cosθ-sinθ=2-
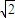
又cos2θ+sin2θ=1
联立得:sin2θ=4
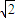 -5=0.656,
-5=0.656,解得:θ=20.5°
所以从MN射出粒子初速方向与x轴正向夹角范围为:[0,20.5°)
点评:带电粒子在磁场中做匀速圆周运动,处理时注意:定圆心、画轨迹、求半径.

练习册系列答案
相关题目
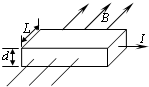 半导体中参与导电的电流载体称为载流子.N型半导体的载流子是带负电的电子,P型半导体的载流子是带正电的“空穴”,如图所示,一块厚度为d、宽度为L的长方形半导体样品,置于方向如图所示、磁感应强度大小为B的匀强磁场中,当半导体样品中通以向右的电流强度为I的恒定电流时,样品上、下底面出现恒定电势差U,且上表面带正电、下表面带负电.设半导体样品中每个载流子带电荷量为q,半导体样品中载流子的密度(单位体积内载流子的个数)用n表示(已知电流I=nqvS,其中v为载流子定向移动的速度,S为导体横截面积),则下列关于样品材料类型的判断和其中载流子密度n大小的表达式正确的是
半导体中参与导电的电流载体称为载流子.N型半导体的载流子是带负电的电子,P型半导体的载流子是带正电的“空穴”,如图所示,一块厚度为d、宽度为L的长方形半导体样品,置于方向如图所示、磁感应强度大小为B的匀强磁场中,当半导体样品中通以向右的电流强度为I的恒定电流时,样品上、下底面出现恒定电势差U,且上表面带正电、下表面带负电.设半导体样品中每个载流子带电荷量为q,半导体样品中载流子的密度(单位体积内载流子的个数)用n表示(已知电流I=nqvS,其中v为载流子定向移动的速度,S为导体横截面积),则下列关于样品材料类型的判断和其中载流子密度n大小的表达式正确的是( )
A、是N型半导体,n=
| ||
B、是P型半导体,n=
| ||
C、是N型半导体,n=
| ||
D、是P型半导体,n=
|
 倾角为α的导电轨道间接有电源,轨道上静止放有一根金属杆ab.现垂直轨道平面向上加一匀强磁场,如图所示,磁感应强度B逐渐增加的过程中,ab杆受到的静摩擦力( )
倾角为α的导电轨道间接有电源,轨道上静止放有一根金属杆ab.现垂直轨道平面向上加一匀强磁场,如图所示,磁感应强度B逐渐增加的过程中,ab杆受到的静摩擦力( ) 截面积为0.2m2的100匝线圈A,处在匀强磁场中,磁场方向垂直于线圈平面,如图所示,磁感应强度B随时间变化的规律为B=0.6-0.02t(T)(t为时间,单位为秒),开始时S未闭合,R1=4Ω,R2=6Ω,C=30μF,线圈电阻不计,求:
截面积为0.2m2的100匝线圈A,处在匀强磁场中,磁场方向垂直于线圈平面,如图所示,磁感应强度B随时间变化的规律为B=0.6-0.02t(T)(t为时间,单位为秒),开始时S未闭合,R1=4Ω,R2=6Ω,C=30μF,线圈电阻不计,求: 如图所示,磁感应强度大小为B=0.15T、方向垂直于纸面向里且分布在半径R=0.10m的圆形磁场区域里,圆的左端和y轴相切于坐标原点O,右端和荧光屏MN相切于x轴上的A点,置于原点O的粒子源可沿x轴正方向发射速度为v=3.0×106m/s的带负电的粒子流,粒子重力不计,比荷为q/m=1.0×108C/kg.现在以过O点且垂直于纸面的直线为轴,将圆形磁场缓慢地顺时针旋转了900,问:(提示:
如图所示,磁感应强度大小为B=0.15T、方向垂直于纸面向里且分布在半径R=0.10m的圆形磁场区域里,圆的左端和y轴相切于坐标原点O,右端和荧光屏MN相切于x轴上的A点,置于原点O的粒子源可沿x轴正方向发射速度为v=3.0×106m/s的带负电的粒子流,粒子重力不计,比荷为q/m=1.0×108C/kg.现在以过O点且垂直于纸面的直线为轴,将圆形磁场缓慢地顺时针旋转了900,问:(提示: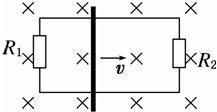 如图所示,在宽为0.5m的平行导轨上垂直导轨放置一个有效电阻为r=0.6Ω的导体棒,在导轨的两端分别连接两个电阻R1=4Ω、R2=6Ω,其他电阻不计.整个装置处在垂直导轨向里的匀强磁场中,如图所示,磁感应强度 B=0.1T.当直导 体棒在导轨上以v=6m/s的速度向右运动时,求:直导体棒两端的电压和流过电阻R1和R2的电流大小.
如图所示,在宽为0.5m的平行导轨上垂直导轨放置一个有效电阻为r=0.6Ω的导体棒,在导轨的两端分别连接两个电阻R1=4Ω、R2=6Ω,其他电阻不计.整个装置处在垂直导轨向里的匀强磁场中,如图所示,磁感应强度 B=0.1T.当直导 体棒在导轨上以v=6m/s的速度向右运动时,求:直导体棒两端的电压和流过电阻R1和R2的电流大小.