题目内容
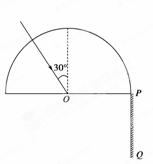
如图所示，半圆形玻璃砖的半径为R，光屏PQ置于直径的右端并与直径垂直，一复色光与竖直方向成α＝30°角射入玻璃砖的圆心，由于色光中含有两种单色光，故在光屏上出现了两个光斑，玻璃对两种单色光的折射率分别为n1＝和n2＝
，求：
①这两个光斑之间的距离；
②为使光屏上的光斑消失，复色光的入射角至少为多少
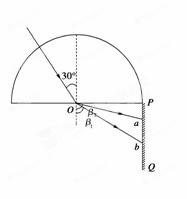
①作出光路如图所示，由折射定律有：n1＝
，n2＝
代入数据得：
＝
＝
解得：β1＝45° β2＝60°
故ab＝Pb－Pa＝Rtan45°－Rtan30°＝(1－
)R
②当两种色光在界面处均发生全反射时光屏上的光斑消失，且玻璃对其折射率为n2的色光先发生全反射，故sinC＝
＝
，即入射角α＝C＝45°.
练习册系列答案
相关题目
如图所示，一玻璃柱体的横截面为半圆形，让太阳光或白炽灯光通过狭缝S形成细光束从空气射向柱体的O点（半圆的圆心），产生反射光束1和透射光束2．现保持入射光不变，将半圆柱绕通过O点垂直于纸面的轴线时针转过，使反射光束1和透射光束2恰好垂直．在入射光线的方向上加偏振片P，偏振片与入射光线垂直，其透振方向在纸面内，这时看到的现象是（ ）
（1）P、Q是一列简谐横波中的质点，相距30m，各自的振动图象如图所示．
如图所示，半圆形玻璃砖放在空气中，三条同一颜色、强度相同的光线，均由空气射入到玻璃砖，到达玻璃的圆心位置．下列说法正确的是（ ）
如图所示，一玻璃柱体的横截面为半圆形，一束细的单色光从空气射向柱体的O点（半圆的圆心），产生反射光束1的透射光束2．已知玻璃折射率为