题目内容
6. 质量为M=2㎏、足够长的木板放在水平面上,现给它一个瞬间冲量,使它获得水平向右的初速度v0=5m/s,在木板右端轻放一个可视为质点的小物块,物块质量m=2㎏.经过0.5s两物体的速度均达到1m/s.设物块与木板之间的最大静摩擦力等于滑动摩擦力,且物块始终在木板上.取重力加速度的大小g=10m/s2,求:
质量为M=2㎏、足够长的木板放在水平面上,现给它一个瞬间冲量,使它获得水平向右的初速度v0=5m/s,在木板右端轻放一个可视为质点的小物块,物块质量m=2㎏.经过0.5s两物体的速度均达到1m/s.设物块与木板之间的最大静摩擦力等于滑动摩擦力,且物块始终在木板上.取重力加速度的大小g=10m/s2,求:(1)物块与木板间、木板与地面间的动摩擦因数;
(2)从t=0时刻到物块与木板均停止运动时,物块相对于木板的位移的大小.
分析 (1)根据运动学的公式,即可求出物块与木板的加速度,然后结合牛顿第二定律即可求出摩擦力的大小,然后由f=μFN求出摩擦因数;
(2)从t=0时刻到物块与木板均停止运动时,由运动学的公式即可求出物块相对于木板的位移.
解答 解:(1)木板做减速运动,加速度为:${a}_{1}=\frac{v-{v}_{0}}{△t}=\frac{1-5}{0.5}=-8$m/s2
物块受到的摩擦力为:f1=ma1=2×(-8)=-16N,负号表示摩擦力的方向与初速度的方向相反;
所以物块与木板之间的动摩擦因数为:${μ}_{1}=\frac{{|f}_{1}|}{mg}=\frac{16}{2×10}=0.8$
物块做加速运动,加速度为:${a}_{2}=\frac{v-0}{△t}=\frac{1-0}{0..5}=2m/{s}^{2}$
木板沿水平方向受到的两个摩擦力的作用,则有:Ma2=-f1+f2
所以:f2=f2+Ma2=-16+2×2=-12N,负号表示摩擦力的方向与物块的初速度的方向相反;
所以地面与木板之间的动摩擦因数为:${μ}_{2}=\frac{{|f}_{2}|}{Mg+mg}=\frac{12}{2×10+2×10}=0.3$
(2)此后,木板受到的地面的摩擦力仍然是12N,若二者一起减速,则加速度为:${a}_{3}=\frac{{f}_{2}}{m+M}=\frac{-12}{2+2}=-3m/{s}^{2}$,负号表示摩擦力的方向与物块的初速度的方向相反;
此时若物块与木板相对静止,则物块与木板之间的摩擦力为:f1′=ma3=2×(-3)=-6N,负号表示摩擦力的方向与物块的初速度的方向相反;
小于物块受到的滑动摩擦力,所以可知此时物块与木板相对静止,没有相对运动.
则只在前0.5s内二者之间有相对运动,前0.5s内物块的位移为:
${x}_{1}=\frac{v+{v}_{0}}{2}•t=\frac{1+5}{2}×0.5=1.5$m
木板的位移为:${x}_{2}=\frac{1}{2}{a}_{2}{t}^{2}=\frac{1}{2}×2×0.{5}^{2}=0.25$m
所以物块相对于木板的位移的大小为:△x=x1-x2=1.5-0.25=1.25m
答:(1)物块与木板间、木板与地面间的动摩擦因数分别是0.8和0.3;
(2)从t=0时刻到物块与木板均停止运动时,物块相对于木板的位移的大小是1.25m.
点评 本题综合考查牛顿第二定律的应用,加速度是联系的纽带.需要注意的是物块与木板的速度相等后,可能相对于木板继续运动,也可能相对于木板静止,要讨论..

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | “爆胎”前随着温度升高,车胎内气体压强将增大 | |
| B. | “爆胎”前随着温度升高,车胎内气体将向外放出热量 | |
| C. | “爆胎”是车胎所有气体分子的动能都急剧增大造成的 | |
| D. | “爆胎”是车胎内气体分子间斥力急剧增大造成的 |
| A. | 水的饱和汽压随体积的升高而增大 | |
| B. | 扩散现象表明,分子在永不停息地运动 | |
| C. | 当分子间距离增大时,分子间引力增大,分子间斥力减小 | |
| D. | 一定质量的理想气体,在等压膨胀过程中,气体分子的平均动能减小 |


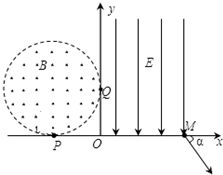 如图所示,在直角坐标系xOy平面的第Ⅱ象限内有半径为R的圆O1分别与x轴、y轴相切于P(-R,0)、Q(0,R) 两点,圆O1内存在垂直于xOy平面向外的匀强磁场,磁感应强度为B.与y轴负方向平行的匀强电场左边界与y轴重合,右边界交x轴于M点,一带正电的粒子A(重力不计)电荷量为q、质量为m,以某一速率垂直于x轴从P点射入磁场,经磁场偏转恰好从Q点进入电场,最后从M点以与x轴正向夹角为45°的方向射出电场.求:
如图所示,在直角坐标系xOy平面的第Ⅱ象限内有半径为R的圆O1分别与x轴、y轴相切于P(-R,0)、Q(0,R) 两点,圆O1内存在垂直于xOy平面向外的匀强磁场,磁感应强度为B.与y轴负方向平行的匀强电场左边界与y轴重合,右边界交x轴于M点,一带正电的粒子A(重力不计)电荷量为q、质量为m,以某一速率垂直于x轴从P点射入磁场,经磁场偏转恰好从Q点进入电场,最后从M点以与x轴正向夹角为45°的方向射出电场.求: