��Ŀ����
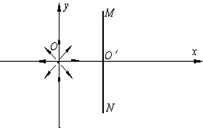 ��ͼ��ʾ����ֱ������ϵ��ԭ��O����һ����Դ�������ܾ��ȷ����ٶȴ�С��ȡ�����ƽ����ֽ��Ĵ������ӣ��ڷ���Դ�ұ���һ�ܱ��ĵ��壬������xoyƽ�潻�ߵ�����M��N��ԭ��O���ù��ɵ���ֱ�������Σ���֪�������ӵ�����Ϊm��������Ϊq���ٶ�Ϊ�ԣ�MN�ij���ΪL������y���Ҳ��һƽ����x�����ǿ�糡��Ҫʹy���Ҳ������˶������Ӷ��ܴ���MN�ϣ���糡ǿ��E0����СֵΪ
��ͼ��ʾ����ֱ������ϵ��ԭ��O����һ����Դ�������ܾ��ȷ����ٶȴ�С��ȡ�����ƽ����ֽ��Ĵ������ӣ��ڷ���Դ�ұ���һ�ܱ��ĵ��壬������xoyƽ�潻�ߵ�����M��N��ԭ��O���ù��ɵ���ֱ�������Σ���֪�������ӵ�����Ϊm��������Ϊq���ٶ�Ϊ�ԣ�MN�ij���ΪL������y���Ҳ��һƽ����x�����ǿ�糡��Ҫʹy���Ҳ������˶������Ӷ��ܴ���MN�ϣ���糡ǿ��E0����СֵΪ������Ҫʹy���Ҳ������˶����Ӷ��ܴ���MN���ϣ����ٽ�����Ϊ����y�᷽���˶�����ƽ���˶������ӣ�ǡ������M��N�㣮����ţ�ٵڶ���������糡ǿ�ȵ���Сֵ�����ݶ��ܶ������������ӵĶ��ܣ�
����⣺������֪��Ҫʹy���Ҳ������˶����Ӷ��ܴ���MN���ϣ����ٽ�����Ϊ����y�᷽���˶�����������ƽ���˶���������M��N�㣮
����ֱ����������������ֱ���˶����У�MO��=
L=vt����
ˮƽ�������������ȼ���ֱ���˶����У�
���ٶ�Ϊ a=
����
OO��=
L=
at2����
��٢ڢ�ʽ�ã�
E0=
����
�ɶ��ܶ���֪��
qE0��
L=Ek-
mv2����
��ܢ�ʽ�ã�
Ek=
mv2
�ʴ�Ϊ��
��
mv2
����ֱ����������������ֱ���˶����У�MO��=
| 1 |
| 2 |
ˮƽ�������������ȼ���ֱ���˶����У�
���ٶ�Ϊ a=
| qE0 |
| m |
OO��=
| 1 |
| 2 |
| 1 |
| 2 |
��٢ڢ�ʽ�ã�
E0=
| 4mv2 |
| qL |
�ɶ��ܶ���֪��
qE0��
| 1 |
| 2 |
| 1 |
| 2 |
��ܢ�ʽ�ã�
Ek=
| 5 |
| 2 |
�ʴ�Ϊ��
| 4mv2 |
| qL |
| 5 |
| 2 |
����������ؼ�Ҫȷ���������е糡ǿ����С����������ȷ�ٽ���������������ڵ糡������ƽ���˶�ʱ��Ҫ�����������˶��ĺϳɺͷֽⷨ�����о���

��ϰ��ϵ�д�
�����Ŀ
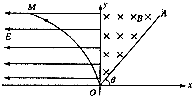 ��ͼ��ʾ����ֱ������ƽ��ĵ�I��������һ��ǿ�ų����Ÿ�Ӧǿ��ΪB��ֱ��OA�Ǵų��Ҳ�ı߽磮�ڵڢ����������ڵ糡ǿ�ȴ�СΪE��ˮƽ�������ǿ�糡��y���ǵ糡���ų�����ķֽ������ߣ�OM���㷽��x=-ky2��k��0������һ�������Ϊq������Ϊm�ĸ����ӣ��������ƣ�������OM��ijһ���ɾ�ֹ�ͷţ���Խy�����ų��У�
��ͼ��ʾ����ֱ������ƽ��ĵ�I��������һ��ǿ�ų����Ÿ�Ӧǿ��ΪB��ֱ��OA�Ǵų��Ҳ�ı߽磮�ڵڢ����������ڵ糡ǿ�ȴ�СΪE��ˮƽ�������ǿ�糡��y���ǵ糡���ų�����ķֽ������ߣ�OM���㷽��x=-ky2��k��0������һ�������Ϊq������Ϊm�ĸ����ӣ��������ƣ�������OM��ijһ���ɾ�ֹ�ͷţ���Խy�����ų��У� ��2013?������ģ����ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶȦ�0��x���������糡����y����Q���뿪�糡ʱ�ٶȱ�Ϊ2��0��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ�ľ�����ǿ�ų�����ͼ��δ���������ӹ�Q������˶�һ�ξ����Ž���ų������ų��Ÿ�Ӧǿ�ȴ�С
��2013?������ģ����ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶȦ�0��x���������糡����y����Q���뿪�糡ʱ�ٶȱ�Ϊ2��0��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ�ľ�����ǿ�ų�����ͼ��δ���������ӹ�Q������˶�һ�ξ����Ž���ų������ų��Ÿ�Ӧǿ�ȴ�С ��ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶ�v0��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��нǦ�=30�㣬Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�СB=
��ͼ��ʾ����ֱ������xOyƽ��y����ࣨ��y�ᣩ��һ��y�Ḻ�����ǿ�糡��һ����Ϊm������Ϊq�Ĵ��������Ӵ�x����P�����ٶ�v0��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��нǦ�=30�㣬Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�СB= ��ͼ��ʾ����ֱ������xoy�ĵ�һ�����зֲ���ָ��y�᷽�����ǿ�糡���ڵ��������зֲ��Ŵ�ֱֽ�����﷽�����ǿ�ų���һ������Ϊm�����磫q������(��������)��A��(0��3)�Գ���V0��120m/sƽ��x������糡����Ȼ��ӵ糡�������ų����ִӴų�����糡������ֻͨ��x���ϵ�P��(6��0)��Q��(8��0)��һ�Σ���֪�����ӵĺ��ʱ�Ϊq/m��108c/kg��
��ͼ��ʾ����ֱ������xoy�ĵ�һ�����зֲ���ָ��y�᷽�����ǿ�糡���ڵ��������зֲ��Ŵ�ֱֽ�����﷽�����ǿ�ų���һ������Ϊm�����磫q������(��������)��A��(0��3)�Գ���V0��120m/sƽ��x������糡����Ȼ��ӵ糡�������ų����ִӴų�����糡������ֻͨ��x���ϵ�P��(6��0)��Q��(8��0)��һ�Σ���֪�����ӵĺ��ʱ�Ϊq/m��108c/kg�� ��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��н�
��x���������糡����y����Q���뿪�糡ʱ�ٶȷ�����y�Ḻ��н� ��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�С
��Q������Ϊ��0��-d������y���Ҳ���һ������ƽ�洹ֱ���н���ǿ�ų�����ͼ��δ���������ų��Ÿ�Ӧǿ�ȴ�С �������ܴ�����ԭ��O��x�Ḻ���ٽ���糡������������������
�������ܴ�����ԭ��O��x�Ḻ���ٽ���糡������������������