题目内容
我国探月工程实施“绕”“落”“回”的发展战略.“绕”即环绕月球进行月表探测;“落”是着月探测;“回”是在月球表面着陆,并采样返回.第一步“绕”已于2007年11月17日成功实现,“嫦娥一号”成功实施第三次近月制动,进入周期为T圆形越极轨道.经过调整后的该圆形越极轨道将是嫦娥一号的最终工作轨道,这条轨道距离月球表面为h,经过月球的南北极上空.已知月球半径为R,万有引力恒量G,(1)求月球的质量M
(2)第二步“落”计划于2012年实现,当飞船在月球表面着陆后,如果宇航员将一小球举高到距月球表面高h处自由释放,求落地时间t.
【答案】分析:研究“嫦娥一号”绕月球做匀速圆周运动,根据万有引力提供向心力,列出等式求出中心体的质量.
在星球表面,运用万有引力等于重力这个思路求出星球表面重力加速度.
根据自由下落的运动规律求出落地时间t.
解答:解:(1)设“嫦娥一号”号的质量为m,根据万有引力提供向心力得:
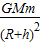 =m(R+h)
=m(R+h)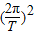
所以:M=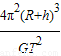
(2)设月球上的加速度为g
不考虑天体的自转,对任何天体表面都可以认为:
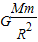 =mg ①,h=
=mg ①,h= gt2 ②
gt2 ②
由①②二式可得t=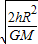 =
=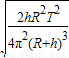
答:(1)月球的质量M为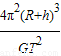
(2)落地时间t为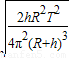 .
.
点评:本题考查了万有引力在天体中的应用,解题的关键在于找出向心力的来源,并能列出等式解题.
不考虑天体的自转,对任何天体表面都可以认为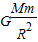 =mg.
=mg.
重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量.
在星球表面,运用万有引力等于重力这个思路求出星球表面重力加速度.
根据自由下落的运动规律求出落地时间t.
解答:解:(1)设“嫦娥一号”号的质量为m,根据万有引力提供向心力得:
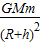 =m(R+h)
=m(R+h)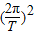
所以:M=
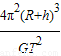
(2)设月球上的加速度为g
不考虑天体的自转,对任何天体表面都可以认为:
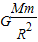 =mg ①,h=
=mg ①,h= gt2 ②
gt2 ②由①②二式可得t=
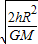 =
=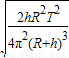
答:(1)月球的质量M为
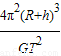
(2)落地时间t为
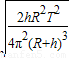 .
.点评:本题考查了万有引力在天体中的应用,解题的关键在于找出向心力的来源,并能列出等式解题.
不考虑天体的自转,对任何天体表面都可以认为
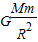 =mg.
=mg.重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目