题目内容
如图所示，A是用轻绳连接的小球，B是用轻杆连接的小球，都在竖直平面内作圆周运动，且绳、杆长度L相等．忽略空气阻力，下面说法中正确的是（ ）| A、A球可能作匀速圆周运动 | ||
B、A球通过圆周最高点最小速度是
| ||
| C、对B球来说，到最低点时处于超重状态，杆对球的作用力最大 | ||
| D、A球在运动过程中所受的合外力的方向处处指向圆心 |
分析：本题中绳系小球A的机械能守恒，做变速圆周运动，合外力方向不一定指向圆心，到最高点时绳子拉力恰好为零时，速度最小，根据牛顿第二定律求解最小速度．B球到达最高点时最小速度为零．根据加速度方向判断B球的状态，确定杆的作用力方向．
解答：解：
A、A球运动过程中，绳子的拉力不做功，机械能守恒，小球的重力势能不断变化，动能就不断变化，速率不断变化，一定做变速圆周运动，故A错误．
B、当A球恰好通过最高点时，绳子的拉力为零，由重力提供向心力，此时速度最小，设为vmin．根据牛顿第二定律得：mg=m
，得；vmin=
；
对于B球，由于杆子对小球能有支撑作用，所以B球过圆周最高点的速度最小可为零，故B正确．
C、对B球来说，到最低点时加速度方向向上，根据牛顿运动定律得知，杆对球的作用力大于重力，B球处于超重状态．
根据牛顿第二定律得：T-mg=m
，T=mg+m
，v最大，T最大，故C正确．
D、A球在运动过程中受到重力和绳子拉力两个作用，根据平行四边形定则可知，A所受的合外力的方向不是处处指向圆心，只有在最高点和最低点两个位置指向圆心，故D错误．
故选：BC
A、A球运动过程中，绳子的拉力不做功，机械能守恒，小球的重力势能不断变化，动能就不断变化，速率不断变化，一定做变速圆周运动，故A错误．
B、当A球恰好通过最高点时，绳子的拉力为零，由重力提供向心力，此时速度最小，设为vmin．根据牛顿第二定律得：mg=m
| ||
| L |
| gL |
对于B球，由于杆子对小球能有支撑作用，所以B球过圆周最高点的速度最小可为零，故B正确．
C、对B球来说，到最低点时加速度方向向上，根据牛顿运动定律得知，杆对球的作用力大于重力，B球处于超重状态．
根据牛顿第二定律得：T-mg=m
| v2 |
| L |
| v2 |
| L |
D、A球在运动过程中受到重力和绳子拉力两个作用，根据平行四边形定则可知，A所受的合外力的方向不是处处指向圆心，只有在最高点和最低点两个位置指向圆心，故D错误．
故选：BC
点评：解决本题的关键知道向心力靠指向圆心的合力来提供，明确绳系模型和轻杆模型最高点的临界条件，根据牛顿第二定律能得到最小速度．
练习册系列答案
相关题目
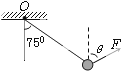（2011?湖南二模）如图所示，一小球用轻绳悬于?点，用力F拉住小球，使悬线保持偏离竖直方向75°角，且小球始终处于平衡状态，为了使F有最小值，F与竖直方向的夹角θ应该是（ ）如图所示，A是用轻绳连接的小球，B是用轻杆连接的小球，都在竖直平面内作圆周运动，且绳、杆长度L相等。忽略空气阻力，下面说法中正确的是
| A．A球可能作匀速圆周运动 |
B．A球通过圆周最高点最小速度是 ，而B球过圆周最高点的速度最小可为零 |
| C．对B球来说，到最低点时处于超重状态，杆对球的作用力最大 |
| D．A球在运动过程中所受的合外力的方向处处指向圆心 |
，而B球过圆周最高点的速度最小可为零
，而B球过圆周最高点的速度最小可为零