题目内容
 如图所示,一汽车后面用细绳拖着质量为m的光滑小球沿水平面向左运动.
如图所示,一汽车后面用细绳拖着质量为m的光滑小球沿水平面向左运动.(1)当汽车以加速度a=
| g |
| 2 |
| 5 |
| 6 |
(2)当汽车以加速度a=g加速运动时,绳的拉力为多大?
分析:(1)分析小球的受力情况,已知加速度,根据牛顿第二定律求解地面对小球的支持力,再由牛顿第三定律得到小球对地面的压力大小.
(2)由牛顿第二定律求出地面对小球刚好没有支持力时的临界加速度,再分析小球的状态,由牛顿第二定律求解绳的拉力大小.
(2)由牛顿第二定律求出地面对小球刚好没有支持力时的临界加速度,再分析小球的状态,由牛顿第二定律求解绳的拉力大小.
解答:解:(1)分析小球的受力情况:重力mg、绳的拉力T,地面的支持力,如图1所示,设绳子与水平方向的夹角为α,根据牛顿第二定律得:
竖直方向:Tsinα+N=mg
水平方向:Tcosα=ma
由题,a=
,T=
mg
联立解得,cosα=0.6,sinα=0.8,N=
mg
(2)设地面对A弹力为零时,物体的临界加速度为a0,则有
mgcotα=ma0,得a0=cotα=
g
∵a=g>a0
∴物体已飘起离开地面,此时物体所受合力为mg,此时小球受力如图2所示,则由三角形知识可知,绳的拉力T′=
=
mg
答:(1)当汽车以加速度a=
加速运动时,绳的拉力为
mg,则此时小球对地面的压力为
mg.
(2)当汽车以加速度a=g加速运动时,绳的拉力为
mg.

竖直方向:Tsinα+N=mg
水平方向:Tcosα=ma
由题,a=
| g |
| 2 |
| 5 |
| 6 |
联立解得,cosα=0.6,sinα=0.8,N=
| 1 |
| 3 |
(2)设地面对A弹力为零时,物体的临界加速度为a0,则有
mgcotα=ma0,得a0=cotα=
| 3 |
| 4 |
∵a=g>a0
∴物体已飘起离开地面,此时物体所受合力为mg,此时小球受力如图2所示,则由三角形知识可知,绳的拉力T′=
| (mg)2+(ma)2 |
| 2 |
答:(1)当汽车以加速度a=
| g |
| 2 |
| 5 |
| 6 |
| 1 |
| 3 |
(2)当汽车以加速度a=g加速运动时,绳的拉力为
| 2 |
点评:本题主要考查了牛顿第二定律的应用,关键是能正确对物体进行受力分析,并结合几何知识求解,难度适中.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 (2009?广州一模)(1)为了安全,在高速公路上行驶的汽车之间应保持必要的距离.已知某段高速公路的最高限速v=108km/h,假设前方车辆突然停止,后面车辆司机从发现这一情况起,经操纵刹车到汽车开始减速经历的时间(即反应时间)t=0.50s,刹车时汽车受到阻力的大小为汽车重力的0.50倍.该段高速公路上以最高限速行驶的汽车,至少应保持的距离为多大?取g=10m/s2.
(2009?广州一模)(1)为了安全,在高速公路上行驶的汽车之间应保持必要的距离.已知某段高速公路的最高限速v=108km/h,假设前方车辆突然停止,后面车辆司机从发现这一情况起,经操纵刹车到汽车开始减速经历的时间(即反应时间)t=0.50s,刹车时汽车受到阻力的大小为汽车重力的0.50倍.该段高速公路上以最高限速行驶的汽车,至少应保持的距离为多大?取g=10m/s2.

 如图所示,一汽车后面用细绳拖着质量为m的光滑小球沿水平面向左运动.
如图所示,一汽车后面用细绳拖着质量为m的光滑小球沿水平面向左运动. 加速运动时,绳的拉力为
加速运动时,绳的拉力为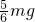 ,则此时小球对地面的压力为多大?
,则此时小球对地面的压力为多大?