题目内容
【题目】如图所示，在边长为a的等边三角形区域内有匀强磁场B ， 其方向垂直纸面向外，一个阻值为R、边长为a的等边三角形导线框架EFG正好与上述磁场区域的边界重合，现使导线框以周期T绕其中心O点在纸面内匀速转动，经过 
导线框转到图中虚线位置，则在这 时间内平均感应电动势 
= ， 通过导线框任一截面的电量q= ． 
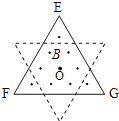
【答案】
；
【解析】两等边三角形所夹的小三角形为等边三角形，小三角形高为：
根据对称性可知，小三角形的底边长为： 
，则小三角形的面积为 
根据法拉第电磁感应定律可知： 
有： 
所以答案是： 
； 
【考点精析】本题主要考查了楞次定律的相关知识点，需要掌握楞次定律适用于一般情况的感应电流方向的判定，而右手定则只适用于导线切割磁感线运动的情况，此种情况用右手定则判定比用楞次定律判定简便才能正确解答此题．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
【题目】一列火车和一辆汽车沿同一方向做匀变速直线运动，速度分别为v1和v2 ． t=0时刻，火车在汽车前方26m处，此后v1、v2在各个时刻的大小如表所示．根据表格中的数据，通过计算求：
t/s | 0 | 1 | 2 | 3 | 4 | 5 |
v1/ms﹣1 | 16.0 | 14.0 | 12.0 | 10.0 | … | … |
v2/ms﹣1 | 4.0 | 5.0 | 6.0 | 7.0 | … | … |
（1）两车经过多长时间相距最大？此时最大间距是多少？
（2）经过多长时间两车相遇？
（3）两车初始间距满足什么条件可以相遇两次．
