题目内容
在地面上竖直上抛一物体,在抛出后第4s内位移的大小是3m,物体能上升的最大高度为多少?
分析:竖直上抛运动是匀变速直线运动,先求解平均速度;平均速度等于中间时刻的瞬时速度,分上升和下降两种情况讨论.
解答:解:竖直上抛运动是匀变速直线运动,在抛出后第4s内位移的大小是3m,故第4s内的平均速度为:
=3m/s;
平均速度等于中间时刻的瞬时速度,故3.5s时刻的速度为3m/s;
①若3.5s时刻的速度向上,则继续上升的时间为:t2=
=0.3s;
故上升的总时间为:t=3.5s+0.3s=3.8s;
故上升的最大高度为:h=
gt2=
×10×3.82=72.2m;
②若3.5s时刻的速度向下,则已经下降的时间为:t′2=
=0.3s;
故上升的总时间为:t=3s-0.3s=2.7s;
故上升的最大高度为:h=
gt2=
×10×2.72=51.2m;
答:物体能上升的最大高度为72.2m或者51.2m.
| 3m |
| 1s |
平均速度等于中间时刻的瞬时速度,故3.5s时刻的速度为3m/s;
①若3.5s时刻的速度向上,则继续上升的时间为:t2=
| 3m/s |
| 10m/s2 |
故上升的总时间为:t=3.5s+0.3s=3.8s;
故上升的最大高度为:h=
| 1 |
| 2 |
| 1 |
| 2 |
②若3.5s时刻的速度向下,则已经下降的时间为:t′2=
| 3m/s |
| 10m/s2 |
故上升的总时间为:t=3s-0.3s=2.7s;
故上升的最大高度为:h=
| 1 |
| 2 |
| 1 |
| 2 |
答:物体能上升的最大高度为72.2m或者51.2m.
点评:本题关键运用平均速度等于中间时刻的瞬时速度得到3.5s时刻的速度大小,然后根据运动学公式分情况列式求解,注意上抛运动的对称性的运用.

练习册系列答案
相关题目
 (2010?济南二模)如图所示,半径R=0.2m的光滑四分之一圆轨道MN竖直固定放置,末端N与一长L=0.8m的水平传送带相切,水平衔接部分摩擦不计,传动轮(轮半径很小)作顺时针转动,带动传送带以恒定的速度ν0运动.传送带离地面的高度h=1.25m,其右侧地面上有一直径D=0.5m的圆形洞,洞口最左端的A点离传送带右端的水平距离S=1m,B点在洞口的最右端.现使质量为m=0.5kg的小物块从M点由静止开始释放,经过传送带后做平抛运动,最终落入洞中,传送带与小物块之间的动摩擦因数μ=0.5. g取10m/s2.求:
(2010?济南二模)如图所示,半径R=0.2m的光滑四分之一圆轨道MN竖直固定放置,末端N与一长L=0.8m的水平传送带相切,水平衔接部分摩擦不计,传动轮(轮半径很小)作顺时针转动,带动传送带以恒定的速度ν0运动.传送带离地面的高度h=1.25m,其右侧地面上有一直径D=0.5m的圆形洞,洞口最左端的A点离传送带右端的水平距离S=1m,B点在洞口的最右端.现使质量为m=0.5kg的小物块从M点由静止开始释放,经过传送带后做平抛运动,最终落入洞中,传送带与小物块之间的动摩擦因数μ=0.5. g取10m/s2.求: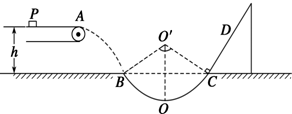 如图所示,水平传送带以5m/s的速度沿顺时针方向运动,在传送带上的P点轻轻地放上一质量m=1kg的小物块,PA间的距离为1.5m,小物块随传送带运动到A点后水平抛出,恰好沿圆弧切线从B点进入竖直光滑圆弧轨道运动.B、C为圆弧的两端点其连线水平,CD为与C点相切的一固定斜面.小物块离开C点后经0.8s通过D点.已知小物块与传送带间的动摩擦因数μ1=0.3,圆弧轨道最低点为O,A点与水平面的高度差h=0.8m,小物块与斜面间的动摩擦因数μ2=
如图所示,水平传送带以5m/s的速度沿顺时针方向运动,在传送带上的P点轻轻地放上一质量m=1kg的小物块,PA间的距离为1.5m,小物块随传送带运动到A点后水平抛出,恰好沿圆弧切线从B点进入竖直光滑圆弧轨道运动.B、C为圆弧的两端点其连线水平,CD为与C点相切的一固定斜面.小物块离开C点后经0.8s通过D点.已知小物块与传送带间的动摩擦因数μ1=0.3,圆弧轨道最低点为O,A点与水平面的高度差h=0.8m,小物块与斜面间的动摩擦因数μ2=