Question

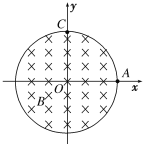
【题目】如图所示，在竖直平面内建立xOy坐标系，在、范围内存在一具有理想边界，方向垂直直面向内的匀强磁场区域。一边长、质量、电阻的匀质正方形刚性导线框abcd处于图示位置，其中心的坐标为。现将线框以初速度水平向右抛出，线框在进入磁场过程中速度保持不变，然后在磁场中运动，最后从磁场右边界离开磁场区域，完成运动全过程。线框在全过程中始终处于xOy平面内，其ab边与x轴保持平行，空气阻力不计。求：

磁感应强度B的大小；

线框在全过程中产生的焦耳热Q；

在全过程中，cb两端的电势差与线框中心位置的x坐标的函数关系。

Answer 1

【答案】（1）2T（2）0.0375J（3）

【解析】

（1）由运动学公式求出线框进入磁场的竖直速度vy，由题意线框进入磁场时速度不变，由平衡条件和欧姆定律就能求出磁感应强度的大小；

（2）由动量定理结合线框通过磁场区域内电量是一定的，恰恰能求出线框的末速度，由能量守恒定律就能求出全过程产生的热量；

（3）分段考虑线框进入磁场时切割磁感线的速度即竖直速度，先表示出电动势，再由欧姆定律表示Ucb两端的电压。

（1）线框进入磁场的过程中速度不变，线框受力平衡：

而感应电流

进入磁场时的y方向速度：

解得：

（2）全过程根据动量定理：

而，联立可得：

而

全过程根据能量守恒定律：

联立解得：

（3）进入磁场前：，，

进入磁场过程

在磁场中

离开磁场过程中

V

故本题答案是：（1）2T（2）0.0375J（3）