Question

如图所示，竖直光滑杆上套有一个小球和两根弹簧，两弹簧的一端各与小球相连，另一端分别用销钉M、N固定于杆上，小球处于静止状态．设拔去销钉M瞬间，小球加速度的大小为12 m/s²，若不拔去销钉M而拔去销钉N瞬间，小球的加速度可能是(取g＝10 m/s²)

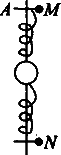
A．22 m/s²，竖直向上

B．22 m/s²，竖直向下

C．2 m/s²，竖直向上

D．2 m/s²，竖直向下

Answer 1

答案：BC
解析：

解析：平衡时两弹簧均处于伸长状态时，FM＝FN＋mg，拔去M后，FN＋mg＝ma＝m×12；拔去N后，FM－mg＝ma，则ma＝FM－mg＝FN＋mg－mg＝ma－mg＝m×2，得a＝2 m/s2，方向向上，C正确． 　　平衡时，M处于伸长状态，N处于压缩状态，则FM＋FN＝mg　①，拔去M后，FM消失，则：FN－mg＝ma＝m×12　②．由①式可判断FN＜mg，由②式判断FN＞mg矛盾，该情况不成立． 　　平衡时，两弹簧均处于压缩状态，则可得：FN＝FM＋mg　①，拔去M后，FN－mg＝ma＝m×12　②，拔去N后，FM＋mg＝ma，则：ma＝FM＋mg＝FN－mg＋mg＝FN＝mg＋m×12＝m×22，a＝22 m/s2，方向竖直向下． 　　点评：判断拔去销钉之前，两弹簧所处的状态是解决该题的关键．除了上述三种情况之外，还有下列几种都是不可能的：①M弹簧压缩，N处于伸长；②M、N均处于原长；③M处于伸长状态，N处于原长状态．①、②两种情况不难判断．对于③，当拔去M，球的加速度将是g，由题意可知，拔去M，球的加速度为12 m/s2＞g，所以③是不可能的．由于弹簧所处的状态不同，因而拔去N出现了多解的可能性．