题目内容
19. 如图所示,质量M=4kg的空箱子,静止放在光滑的水平面上,箱子中有一个质量m=2kg的铁块,铁块与箱子的左端ab壁相距x=2m,它一旦与ab壁接触后就不会再分开,铁块与箱底间的动摩擦因数为0.1,现用水平向右的恒力F=10N作用于箱子,在2s末立即撤去作用力F,g=10m/s2,则:
如图所示,质量M=4kg的空箱子,静止放在光滑的水平面上,箱子中有一个质量m=2kg的铁块,铁块与箱子的左端ab壁相距x=2m,它一旦与ab壁接触后就不会再分开,铁块与箱底间的动摩擦因数为0.1,现用水平向右的恒力F=10N作用于箱子,在2s末立即撤去作用力F,g=10m/s2,则:(1)在2s内箱子的加速度多大?
(2)最后,箱子与铁块的速度各为多大?(保留两位有效数字)
分析 (1)先要判断铁块能否木箱一起加速.由整体法求得加速度,再隔离物块求出两者相对静止时的最大加速度,从而判断出铁块与木箱相对运动,即可根据牛顿第二定律求箱子的加速度.
(2)由速度公式求出2s末箱子的速度,由位移公式求出箱子在2s内的位移.对铁块,由牛顿第二定律求出匀加速运动的加速度.由速度公式求出2s末的速度,由位移公式求出2s内的位移.撤去F后,当箱子与铁块的位移等于x=2m时,铁块与箱子发生碰撞,由位移关系求出撤去F后到两者相撞的时间,由速度公式求出碰撞前两者的速度,再由动量守恒定律求碰后的共同速度.
解答 解:(1)假设箱子和铁块一起加速运动,由整体法得整体的加速度 a0=$\frac{F}{M+m}$=$\frac{10}{4+2}$=$\frac{5}{3}$m/s2.
铁块的最大加速度为 am=$\frac{μmg}{m}$=μg=1m/s2
因为am<a0,所以箱子和铁块发生相对滑动
对箱子,由牛顿第二定律得箱子的加速度:a1=$\frac{F-μmg}{M}$=$\frac{10-0.1×2×10}{4}$=2m/s2
(2)在2s末,箱子的末速度大小为:v1=a1t=2×2=4m/s
箱子的位移:x1=$\frac{1}{2}$a1t2=$\frac{1}{2}$×2×22m=4m
对铁块:加速度 a2=$\frac{μmg}{m}$=μg=1m/s2
在2s末,铁块的末速度大小为:v2=a2t=1×2=2m/s
铁块的位移:x2=$\frac{1}{2}$a2t2=$\frac{1}{2}$×1×22m=2m
可知 x1-x2=x
则2s末铁块和箱子相碰,两者将结合在一起.
取向右为正方向,设碰后共同速度为v,根据动量守恒定律得:Mv1+mv2=(M+m)v
可得:v≈3.3m/s
答:
(1)在2s内箱子的加速度为2m/s2.
(2)最后,箱子与铁块的速度均为3.3m/s.
点评 该题将牛顿运动定律与动量守恒定律结合起来,关键要分析清楚物体的运动过程,抓住碰撞过程的基本规律进行求解.

 P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星S1、S2做匀速圆周运动,图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同,则( )
P1、P2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星S1、S2做匀速圆周运动,图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a,横坐标表示物体到行星中心的距离r的平方,两条曲线分别表示P1、P2周围的a与r2的反比关系,它们左端点横坐标相同,则( )| A. | P1的半径大于P2的半径 | B. | P1的质量比P2的质量小 | ||
| C. | S1的线速度比S2的线速度大 | D. | S1的公转周期比S2的大 |

| A. | 图是用来研究涡流现象的实验电路 | |
| B. | 开关S闭合瞬间,灯泡A立即亮起来 | |
| C. | 开关S断开瞬间,P点电势比Q点电势高 | |
| D. | 干电池的左端为电源的正极 |
 一质点沿x轴正方向做直线运动,通过坐标原点时开始计时,其$\frac{x}{t}$-t图象如图所示,下列说法正确的是( )
一质点沿x轴正方向做直线运动,通过坐标原点时开始计时,其$\frac{x}{t}$-t图象如图所示,下列说法正确的是( )| A. | 质点做匀速直线运动,速度为0.5m/s | |
| B. | 质点做匀加速直线运动,加速度为0.5m/s2 | |
| C. | 质点在第1s内的平均速度为1.0m/s | |
| D. | 质点在第1s末的速度为1.0m/s |
| A. | 飞机轮胎用导电橡胶制成是为了避免静电对飞机造成危害 | |
| B. | 探测地雷的探测器是利用静电现象来工作的 | |
| C. | 利用涡流可以冶炼高质量的合金 | |
| D. | 在变压器中减小涡流损失能量的途径之一是减小铁芯材料的电阻率 |
 如图所示,固定于水平面的两足够长的光滑平行金属导轨PMN、P′M′N′,由倾斜和水平两部分在M、M′处平滑连接组成,导轨间距L=1m,水平部分处于竖直向上的匀强磁场中,磁感应强度B=1T.金属棒a、b垂直于倾斜导轨放置,质量均为m=0.2kg,a的电阻R1=1Ω,b的电阻R2=3Ω,a、b长度均为L=1m,棒a距水平面的高度h1=0.45m,棒b距水平面的高度为h2(h2>h1);保持b棒静止,由静止释放a棒,a棒到达磁场中OO′停止运动,后再由静止释放b棒,a、b与导轨接触良好且导轨电阻不计,重力加速度g=10m/s2.
如图所示,固定于水平面的两足够长的光滑平行金属导轨PMN、P′M′N′,由倾斜和水平两部分在M、M′处平滑连接组成,导轨间距L=1m,水平部分处于竖直向上的匀强磁场中,磁感应强度B=1T.金属棒a、b垂直于倾斜导轨放置,质量均为m=0.2kg,a的电阻R1=1Ω,b的电阻R2=3Ω,a、b长度均为L=1m,棒a距水平面的高度h1=0.45m,棒b距水平面的高度为h2(h2>h1);保持b棒静止,由静止释放a棒,a棒到达磁场中OO′停止运动,后再由静止释放b棒,a、b与导轨接触良好且导轨电阻不计,重力加速度g=10m/s2.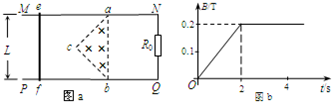
 如图所示,已知物体与水平面的摩擦因数μ=0.2,质量为5kg的物块在水平拉力F=15N的作用下,从静止开始向右运动.(g=10m/s2)求:
如图所示,已知物体与水平面的摩擦因数μ=0.2,质量为5kg的物块在水平拉力F=15N的作用下,从静止开始向右运动.(g=10m/s2)求: