��Ŀ����
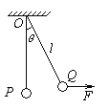
����Ŀ����ͼa��ʾ��ˮƽֱ��MN�·�����ֱ���ϵ���ǿ�糡���ֽ�һ�������ơ��Ⱥ�![]() ����������ڵ糡�е�O���ɾ�ֹ�ͷţ�����
����������ڵ糡�е�O���ɾ�ֹ�ͷţ�����![]() �����
�����![]() ���ٶ�ͨ��MN�������Ϸ�����ǿ�ų����ų���ֽ�洹ֱ���Ÿ�Ӧǿ��B��ͼb��ʾ���������Ա仯��ͼb�дų��Դ�ֱֽ������Ϊ�����Ե�ɵ�һ��ͨ��MNʱΪt=0ʱ�̣�����������������ʾ��
���ٶ�ͨ��MN�������Ϸ�����ǿ�ų����ų���ֽ�洹ֱ���Ÿ�Ӧǿ��B��ͼb��ʾ���������Ա仯��ͼb�дų��Դ�ֱֽ������Ϊ�����Ե�ɵ�һ��ͨ��MNʱΪt=0ʱ�̣�����������������ʾ��
(1)�������������ų�����ų����˶��İ뾶�����ڣ�
(2)�����O���ҷ�47.5cm����һ��ֱ��MN���㹻��ĵ��壬���ɴ�O������˶������������ʱ�䡣

���𰸡�(1)5cm��![]() ��3cm��
��3cm��![]() ��(2)
��(2)![]()
��������
(1)���ų���ֱֽ������ʱ�������˶��İ뾶Ϊ![]()
��
![]()
��
![]()
���ų���ֱֽ������ʱ�������˶��İ뾶Ϊ![]()
![]()
��Բ���˶����ɵ�
![]()
���ų���ֱֽ������ʱ������
![]()
���ų���ֱֽ������ʱ������
![]()
(2)�ʵ�ɴ�![]() ʱ�̿�ʼ���������˶�����ϴų��������Կ�֪�˶��켣��ͼ��ʾ
ʱ�̿�ʼ���������˶�����ϴų��������Կ�֪�˶��켣��ͼ��ʾ

��ɵ�һ��ͨ��MN��ʼ�����˶�������
![]()
��ʱ���Ӿ���![]() ���ˮƽ����Ϊ
���ˮƽ����Ϊ
![]()
��ÿ����һ�����ڣ�������ˮƽ��������ǰ��![]() �����ݵ�ɵ��˶������֪����ɵ��ﵲ��ǰ�˶�������������Ϊ10������
�����ݵ�ɵ��˶������֪����ɵ��ﵲ��ǰ�˶�������������Ϊ10������
![]()
�����7.5cm�ľ�����ͼ��ʾ

��
![]()
���
![]()
��
![]()
�ʵ���˶�����ʱ��
![]()

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ