Question

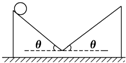伽利略曾利用对接斜面研究“力与运动”的关系．如图，固定在水平地面上的倾角均为θ的两斜面，以光滑小圆弧相连接，左侧顶端有一小球，与两斜面的动摩擦因数均为μ．小球从左侧顶端滑到最低点的时间为t₁，滑到右侧最高点的时间为t₂．规定斜面连接处为参考平面，则小球在这个运动过程中速度的大小v、加速度的大小a、动能E_k及机械能E随时间t变化的关系图线正确的是（　　）

• A、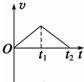
• B、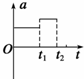
• C、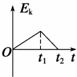
• D、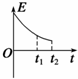

Answer 1

分析：据牛顿第二定律求出上滑和下滑过程中的加速度大小，从而得出速度随时间的变化规律，根据动能与速度大小的关系得出动能与时间t变化的关系求解．

解答：解：A、由牛顿第二定律可知，小球在两斜面的运动都是匀变速直线运动，两阶段的加速度都恒定不变，
小球在左侧斜面下滑时的加速度：a₁=gsinθ-μgcosθ
小球在右侧斜面下滑时的加速度：a₂=gsinθ+μgcosθ，
小球在左侧斜面下滑时的加速度较小，故A错误，B正确；
C、小球的动能与速率的二次方成正比，即E_k=

1

2

mv²，因此，动能与时间关系图象是曲线，故C错误；
D、由于小球在两斜面运动时的加速度大小不相等，因此，小球机械能与时间的关系图象不是连续曲线，故D错误；
故选：B．

点评：解决本题的关键根据牛顿第二定律得出上滑和下滑的加速度，判断出物体的运动情况．