题目内容
宇骯员在月球表面完成下面实验：在一固定的竖直光滑圆弧轨道内部最低点静止一质量为m球（可视为质点）如图所示，当施加给小球一瞬时水平冲量I，刚好能使小球在竖直面内做完整圆周运动。已知圆弧轨道半径为r,月球的半径为R,万有引力常量为G。求：
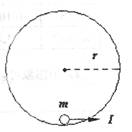
（1)若在月球表面上发射一颗环月卫星，所需最小的发射速度为多大？
(2) 轨道半径为2R的环月卫星周期为多大？
【答案】
解：设月球表面重力加速度为g，月球质量为M
在圆弧最低点对小球有：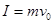 
①（1分）
因为球刚好完成圆周运动，所以小球在最高点有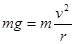
②（2分）
从最低点至最高低点有：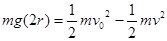
③（2分）
由①②③可得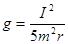 
（2分）
因为在月球发射卫星的最小速度等于月球近地卫星的环绕速度
由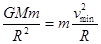 
④ （2分）
并将黄金代换式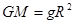 
代入④式
（1分）
得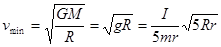
（2分）
（2）当环月卫星轨道半径为2R时，有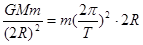
⑤（2分）
得 
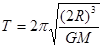⑥（2分）
将黄金代换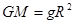式 代入⑥式
得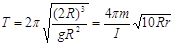 
（2分）
【解析】略
练习册系列答案
名校课堂系列答案
相关题目