题目内容
13. 如图所示是磁带录音机的磁带盒的示意图,A、B为缠绕磁带的两个轮子,其半径均为r.在放音结束时,磁带全部绕到了B轮上,磁带的外缘半径为R,且R=3r.现在进行倒带,使磁带绕到A轮上.倒带时A轮是主动轮,其转速是恒定的,B轮是从动轮.经测定磁带全部绕到A轮上需要的时间为t.则从开始倒带到A、B两轮的转速相等所需要的时间$\frac{\sqrt{5}-1}{2}t$.
如图所示是磁带录音机的磁带盒的示意图,A、B为缠绕磁带的两个轮子,其半径均为r.在放音结束时,磁带全部绕到了B轮上,磁带的外缘半径为R,且R=3r.现在进行倒带,使磁带绕到A轮上.倒带时A轮是主动轮,其转速是恒定的,B轮是从动轮.经测定磁带全部绕到A轮上需要的时间为t.则从开始倒带到A、B两轮的转速相等所需要的时间$\frac{\sqrt{5}-1}{2}t$.
分析 主动轮和从动轮边缘上的点线速度相等,A的角速度恒定,半径增大,线速度增大,当两轮半径相等时,角速度相等.
解答 解:在A轮转动的过程中,半径均匀增大,角速度恒定,根据v=rω,知线速度均匀增大,设从开始倒带到A、B两轮的角速度相等所需要的时间为t′,此时磁带边缘上各点的速度大小为v.
将磁带边缘上各点的运动等效看成一种匀加速直线运动,加速度为a,磁带总长为L,则:
则有:v2-(rω)2=(3rω)2-v2=2a•$\frac{L}{2}$
得:v=$\sqrt{5}$rω
结合加速度的定义得:
$\frac{v-rω}{t′}$=$\frac{3rω-rω}{t}$
代入得:
$\frac{\sqrt{5}rω-rω}{t′}$=$\frac{3rω-rω}{t}$
解得:t′=$\frac{\sqrt{5}-1}{2}t$;
故答案为:$\frac{\sqrt{5}-1}{2}t$.
点评 解决本题的关键要灵活运用等效法,将磁带边缘上点的运动与匀加速直线运动等效,建立模型,可理清思路,同时要知道线速度与角速度的关系,以及知道A、B两轮的角速度相等时,半径相等.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
3. 如图所示,匀强磁场方向垂直于线圈平面,先后两次将线框从同一位置匀速地拉出有界磁场,第一次速度v1=v,第二次速度v2=2v,在先、后两次过程中,正确的是( )
如图所示,匀强磁场方向垂直于线圈平面,先后两次将线框从同一位置匀速地拉出有界磁场,第一次速度v1=v,第二次速度v2=2v,在先、后两次过程中,正确的是( )
 如图所示,匀强磁场方向垂直于线圈平面,先后两次将线框从同一位置匀速地拉出有界磁场,第一次速度v1=v,第二次速度v2=2v,在先、后两次过程中,正确的是( )
如图所示,匀强磁场方向垂直于线圈平面,先后两次将线框从同一位置匀速地拉出有界磁场,第一次速度v1=v,第二次速度v2=2v,在先、后两次过程中,正确的是( )| A. | 线框中感应电流之比为1:2 | |
| B. | 线框中产生热量之比为1:2 | |
| C. | 沿运动方向作用在线框上的外力的功率之比为1:2 | |
| D. | 通过线圈横截面的电荷量之比1:2 |
3.关于分子间的作用力,下列说法正确的是( )
| A. | 分子之间的斥力和引力同时存在 | |
| B. | 分子之间的斥力和引力大小都随分子间距离的增大而减小 | |
| C. | 分子之间的距离减小时,分子力一直做正功 | |
| D. | 分子之间的距离增大时,分子势能一直减小 | |
| E. | 分子之间的距离增大时,可能存在分子势能相等的两个点 |
10. 一列简谐横波在t=0时刻的波形图如图中实线所示,从此刻起,经0.1s波形图如图中虚线所示,若波传播的速度为10m/s,则
一列简谐横波在t=0时刻的波形图如图中实线所示,从此刻起,经0.1s波形图如图中虚线所示,若波传播的速度为10m/s,则
( )
 一列简谐横波在t=0时刻的波形图如图中实线所示,从此刻起,经0.1s波形图如图中虚线所示,若波传播的速度为10m/s,则
一列简谐横波在t=0时刻的波形图如图中实线所示,从此刻起,经0.1s波形图如图中虚线所示,若波传播的速度为10m/s,则( )
| A. | 这列波沿x轴正方向传播 | |
| B. | t=0时刻质点a沿y轴正方向运动 | |
| C. | 从t=0时刻开始质点a经0.2s通过的路程为0.4m | |
| D. | x=2m处的质点的位移表达式为y=0.2sin(5πt-π)(m) |
7. 如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数为n2=100匝,将原线圈接在u=110$\sqrt{2}$sin120πtV的交流电源上,电阻R=100Ω,电力表A为理想电表,下列判断正确的是( )
如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数为n2=100匝,将原线圈接在u=110$\sqrt{2}$sin120πtV的交流电源上,电阻R=100Ω,电力表A为理想电表,下列判断正确的是( )
 如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数为n2=100匝,将原线圈接在u=110$\sqrt{2}$sin120πtV的交流电源上,电阻R=100Ω,电力表A为理想电表,下列判断正确的是( )
如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数为n2=100匝,将原线圈接在u=110$\sqrt{2}$sin120πtV的交流电源上,电阻R=100Ω,电力表A为理想电表,下列判断正确的是( )| A. | 交流电的频率为60Hz | |
| B. | 电流表A的示数为0.1A | |
| C. | 变压器的输入功率是1W | |
| D. | 穿过铁芯的磁通量的最大变化率为$\frac{1}{1200π}$Wb/s |
8.用牛顿第三定律判断下列说法正确的是( )
| A. | 一个作用力和它的反作用力的合力刚好为零 | |
| B. | 静止物体与运动物体之间不存在着作用力与反作用力 | |
| C. | 划船时用船桨向后划水,水同时给船桨一个反作用力推动船前进 | |
| D. | 运动员在起跑加速阶段,地面对运动员的摩擦力大于运动员对地面的摩擦力 |
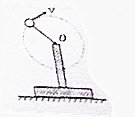 如图所示,长为L=1m的轻质木材,一端固定一个质量m=2kg的小球,以支架上的O点为轴在竖直面内做圆周运动,支架质量M=5kg,当小球运动到最高点时v=2m/s,则此时支架对地面的压力为多少?若要使支架对地面的压力为零,则小球运动到最高点时速度又该为多少?(g取10m/s2)
如图所示,长为L=1m的轻质木材,一端固定一个质量m=2kg的小球,以支架上的O点为轴在竖直面内做圆周运动,支架质量M=5kg,当小球运动到最高点时v=2m/s,则此时支架对地面的压力为多少?若要使支架对地面的压力为零,则小球运动到最高点时速度又该为多少?(g取10m/s2) 如图表示一个摆的运动,摆长为l,摆球质量为m,开始时,线与竖直方向成30°角,小球由静止释放,求小球到达最低点时对线的拉力.
如图表示一个摆的运动,摆长为l,摆球质量为m,开始时,线与竖直方向成30°角,小球由静止释放,求小球到达最低点时对线的拉力. 如图所示,质量均为m的小球A和B,球B置于光滑水平面上,当球A从高为h处由静止摆下,到达最低点恰好与B相碰,并粘合在一起继续摆动,绳长为l.求:
如图所示,质量均为m的小球A和B,球B置于光滑水平面上,当球A从高为h处由静止摆下,到达最低点恰好与B相碰,并粘合在一起继续摆动,绳长为l.求: