Question

(18分)如图所示，长为L的不可伸长的绳子一端固定在O点，另一端系质量为m的小球，小球静止在光滑水平面上。现用大小为F水平恒力作用在另一质量为2m的物块上，使其从静止开始向右运动，一段时间后撤去该力，物块与小球发生正碰后速度大小变为原来的一半而速度方向不变，小球恰好能在竖直平面内做圆周运动。已知重力加速度为，小球和物体均可视为质点，试求:

(1)小物块碰撞前速度的大小；

(2)恒力F作用时间。

 

Answer 1

【答案】

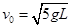   (1)    (2)

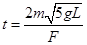
【解析】

试题分析：(1)小球恰好通过最高点作圆周运动，此时重力刚好提供向心力，设速度为，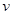

有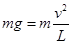：，即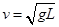

设小球碰撞后速度为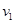，其后在摆至最高点过程中，机械能守恒：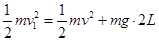

联立可得：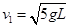

 碰撞过程中，物块和小球的系统动量守恒，有：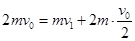

代入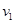值可得：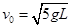 

（3）小球在水平面运动的加速度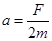 

由速度公式得：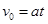  

力F作用时间为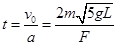 

考点：本题考查了圆周运动规律、机械能守恒定律、动量守恒定律运动学公式。