题目内容
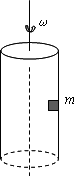
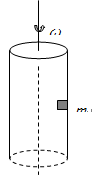
 如图所示,一个中空的圆柱体在水平面内绕轴匀速转动,一个质量m=0.2kg的物块(看做质点)紧贴圆柱内壁随圆柱一起转动,但不与圆柱内壁粘连.已知圆柱体内径d=1.0m,物块与内壁的动摩擦因数μ=0.4,假设最大静摩擦力等于滑动摩擦力.要使物块与圆柱体保持相对静止,求圆柱体绕中心轴旋转的角速度ω的范围.(g=10m/s2)
如图所示,一个中空的圆柱体在水平面内绕轴匀速转动,一个质量m=0.2kg的物块(看做质点)紧贴圆柱内壁随圆柱一起转动,但不与圆柱内壁粘连.已知圆柱体内径d=1.0m,物块与内壁的动摩擦因数μ=0.4,假设最大静摩擦力等于滑动摩擦力.要使物块与圆柱体保持相对静止,求圆柱体绕中心轴旋转的角速度ω的范围.(g=10m/s2)分析:受力分析可知,物块受到三个力,水平方向上的筒壁的弹力、竖直向下的重力和竖直向上的摩擦力.先求临界值,此时重力和摩擦力平衡,弹力完全用力提供向心力,列方程求解即可.
解答:解:对物块做受力分析可知,要使物块不滑下的最小向心力完全由内壁弹力提供F向=N=mrω2
其中r=
在竖直方向上重力和摩擦力是一对平衡力,f=μN=mg
由上面三式,带入数据后得:ω=5
rad/s
所以角速度的范围为:ω≥5
rad/s
答:圆柱体绕中心轴旋转的角速度ω的范围应ω≥5
rad/s.
其中r=
| d |
| 2 |
在竖直方向上重力和摩擦力是一对平衡力,f=μN=mg
由上面三式,带入数据后得:ω=5
| 2 |
所以角速度的范围为:ω≥5
| 2 |
答:圆柱体绕中心轴旋转的角速度ω的范围应ω≥5
| 2 |
点评:正确的受力分析是解决此题的关键,重力和摩擦力平衡,弹力提供向心力.难度不大,属于中档题.

练习册系列答案
相关题目