��Ŀ����
����Ŀ�������Ϊ�ȵĹ⻬б�������������ᵯ�����ӵ����A��B�����ǵ������ֱ�Ϊm��2m�����ɵľ���ϵ��Ϊk��CΪһ�̶����壬ϵͳ���ھ�ֹ״̬������һ��б�淽��ĺ��������Aʹ֮��б�������˶�����B���뿪Cʱ��A���ٶ�Ϊv�����ٶȷ�����б�����ϣ���СΪa���� ��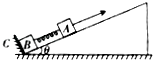
A.�Ӿ�ֹ��B���뿪C�Ĺ����У�A������λ��Ϊ ![]()
B.�Ӿ�ֹ��B���뿪C�Ĺ����У�������A���Ĺ�Ϊ�� ![]()
C.B���뿪Cʱ��������A�����Ĺ���Ϊ��mgsin��+ma��v
D.��A���ٶȴﵽ���ʱ��B�ļ��ٶȴ�СΪ ![]()
���𰸡�A,D
���������⣺A����ʼʱ�����ɴ���ѹ��״̬��ѹ����������A�������»����������ݺ��˶��ɣ��У�
mgsin��=kx1
��ã�x1= ![]()
���B��Ҫ�뿪Cʱ�����ɵ�������������B�������»����������ݺ��˶��ɣ��У�
2mgsin��=kx2
��ã�x2= ![]()
�����A�˶��ľ���Ϊ�� ![]() ��A�������⣻
��A�������⣻
B���Ӿ�ֹ��B���뿪C�Ĺ����У����A�˷���������Ϊ ![]() ��B���������⣻
��B���������⣻
C����ʱ����A��������������֧�����͵��ɵ�����������ţ�ٵڶ����ɣ��У�
F��mgsin�ȩ�T=ma
���ɵ�������������B�������»�������Ϊ��
T=2mgsin��
�ʣ�F=3mgsin��+ma��������A�����Ĺ���Ϊ��3mgsin��+ma��v��C���������⣻
D����A���ٶȴﵽ���ʱ��A�ܵ��ĺ�����Ϊ0����F��mgsin�ȩ�T��=0
���ԣ�T��=2mgsin��+ma
B��б�淽���ܵ�������FB=T�䩁2mgsin��=ma
�֣�FB=2ma��
���ԣ� ![]() ��D�������⣮
��D�������⣮
���Դ��ǣ�AD
�����㾫����������Ҫ�����˺����������ʵļ�������������֪ʶ�㣬��Ҫ���պ����Ĺ��ɸ���W=F��S��cos�Ƚ��м��㣬����ʽֻ�����ں������������ʵļ��㣺 P = W/tW ��ʾ������λ�ǽ���J��. t��ʾʱ�� ����λ���루s�� P��ʾ���ʣ���λ�����أ�W��1 W= 1 J/s������ȷ�����⣮