题目内容
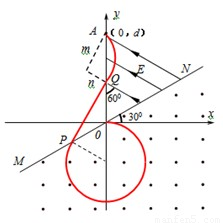
(12分)如图所示,在xoy平面内,直线MN与x轴正方向成30o角,MN下方是垂直于纸面向外的匀强磁场,MN与y轴正方向间存在电场强度E=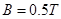 ×105N/C的匀强电场,其方向与y轴正方向成60o角且指向左上方,一重力不计的带正电粒子,从坐标原点O沿x轴正方向进入磁场,已知粒子的比荷
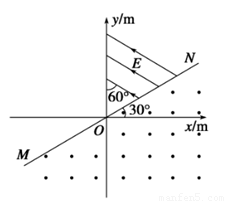
×105N/C的匀强电场,其方向与y轴正方向成60o角且指向左上方,一重力不计的带正电粒子,从坐标原点O沿x轴正方向进入磁场,已知粒子的比荷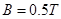 =107C/kg,结果均保留两位有效数字,试问:
=107C/kg,结果均保留两位有效数字,试问:
(1)若测得该粒子经过磁场的时间t1=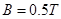 ,求磁感应强度的大小B;
,求磁感应强度的大小B;
(2)若测得该粒子经过磁场的时间t1=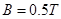 ,粒子从坐标原点开始到第一次到达y轴正半轴的时间t
,粒子从坐标原点开始到第一次到达y轴正半轴的时间t
(3)若粒子的速度v0=1.0×106m/s,求粒子进入电场后最终离开电场时的位置坐标
【答案】
(1)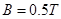 (2)
(2)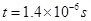 (3)
(3)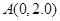
【解析】
试题分析:(1)由几何关系可知: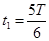 ,又
,又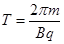 联立可得
联立可得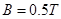
(2)设粒子在磁场中的运动半径为r,速度为v,由几何关系可知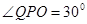 ,POQ为等腰三角形,所以
,POQ为等腰三角形,所以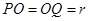 ,
,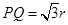 ,故
,故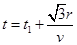 ,
,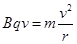 ,联立可得
,联立可得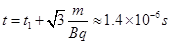
(3)粒子进入电场后做类平抛运动,设垂直于电场方向的距离为m,电场方向的距离为n,粒子离开电场时经过y轴,其位置坐标为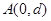 ,所以
,所以
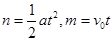 ,
,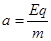 ,解得
,解得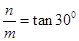 ,又
,又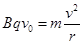 ,所以
,所以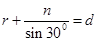 ,
,
联立可得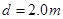
考点:考查了牛顿运动定律与电磁线综合,能力性非常的高,注意粒子的运动过程

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?
(3)金属棒从释放到落地过程中在电子元件上消耗的电能多大? 等效电阻
等效电阻 ,式中k为恒量。框架上有一质量为m的金属棒水平放置,金属棒与光滑框架接触良好,离地高为h,磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放,棒沿框架向下运动。其它电阻不计,问:
,式中k为恒量。框架上有一质量为m的金属棒水平放置,金属棒与光滑框架接触良好,离地高为h,磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放,棒沿框架向下运动。其它电阻不计,问: (3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?
(3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?

 ,S断开时,电压表示数为16V,S闭合时,电压表示数为10V,若电压表可视为理想的,则电源电动势和内电阻为多少?
,S断开时,电压表示数为16V,S闭合时,电压表示数为10V,若电压表可视为理想的,则电源电动势和内电阻为多少?