题目内容
质量为m的物体放在水平面上,在沿水平方向大小为F的拉力(F<mg)作用下做匀速运动,如图所示.试求:(1)物体与水平面间的动摩擦因数
(2)在物体上再施加另一个大小为F的力,
①若要使物体仍沿原方向做匀速运动,该力的方向如何?
②若要使物体沿原方向移动距离s后动能的增加最大,该力的方向如何?

【答案】分析:(1)对物体进行受力分析,根据平衡条件列式即可求解动摩擦因素;
(2)施加的力F分斜向上和斜向下两种情况,根据平衡条件列式即可求解方向;
(3)由动能定理可知道,△Ek=F合?scosθ,因s一定,F合有最大值时最△Ek最大.设后来所加的外力F斜向右上方且与水平方向的夹角为θ,求出合力的表达式,结合数学知识求解最大值即可.
解答:解: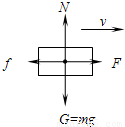 (1)物体的受力如图所示,由物体做匀速运动得
(1)物体的受力如图所示,由物体做匀速运动得
F-f=0
N-mg=0
f=μN
解得: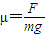
(2)分两种情形:
①设所加的力F斜向右下方,且与水平方向的夹角为θ,由物体做匀速运动得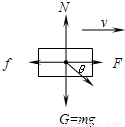
F+Fcosθ-f=0
N-mg-Fsinθ=0
f=μN
由以上三式可以推得,
Fcosθ=μFsinθ
tanθ=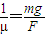 ,即θ=arctan=
,即θ=arctan=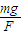
②设所加的力F斜向左上方,且与水平方向的夹角为θ,由物体做匀速运动得知
F-Fcosθ-f=0
N+Fsinθ-mg=0
f=μN
解得
tanθ=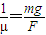 ,即θ=arctan
,即θ=arctan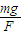
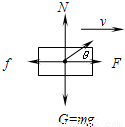
故所加外力F与水平面的夹角为arctan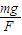 ,斜向右下方或左上方.
,斜向右下方或左上方.
(3)由动能定理可知道,△Ek=F合?scosθ,因s一定,F合有最大值时最△Ek最大.
设后来所加的外力F斜向右上方且与水平方向的夹角为θ,则
物体所受的合力为F合=F+Fcosθ-f=0
在竖直方向Fsinθ+N-mg=0
由摩擦定律 f=μN
解得F合=F(cosθ+μsinθ)
令tanα=μ,则
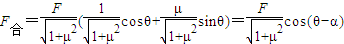
由上式可知当cos(θ-α)=1,α=θ=arctan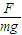 ,
,
即所加外力斜向右上方与水平夹角为arctan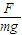 时
时
F取最大值Fmax=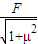
答:1)物体与水平面间的动摩擦因数为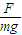 ;
;
(2)在物体上再施加另一个大小为F的力,
①若要使物体仍沿原方向做匀速运动,所加外力F与水平面的夹角为arctan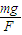 ,斜向右下方或左上方;
,斜向右下方或左上方;
②若要使物体沿原方向移动距离s后动能的增加最大,所加外力斜向右上方与水平夹角为arctan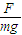 .
.
点评:本题主要考查了同学们受力分析的能力,要求同学们能根据平衡条件列式求解,知道s一定时,F合有最大值时最△Ek最大,难度适中.
(2)施加的力F分斜向上和斜向下两种情况,根据平衡条件列式即可求解方向;
(3)由动能定理可知道,△Ek=F合?scosθ,因s一定,F合有最大值时最△Ek最大.设后来所加的外力F斜向右上方且与水平方向的夹角为θ,求出合力的表达式,结合数学知识求解最大值即可.
解答:解:
 (1)物体的受力如图所示,由物体做匀速运动得
(1)物体的受力如图所示,由物体做匀速运动得F-f=0
N-mg=0
f=μN
解得:
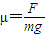
(2)分两种情形:
①设所加的力F斜向右下方,且与水平方向的夹角为θ,由物体做匀速运动得

F+Fcosθ-f=0
N-mg-Fsinθ=0
f=μN
由以上三式可以推得,
Fcosθ=μFsinθ
tanθ=
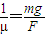 ,即θ=arctan=
,即θ=arctan=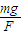
②设所加的力F斜向左上方,且与水平方向的夹角为θ,由物体做匀速运动得知
F-Fcosθ-f=0
N+Fsinθ-mg=0
f=μN
解得
tanθ=
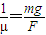 ,即θ=arctan
,即θ=arctan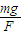
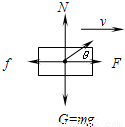
故所加外力F与水平面的夹角为arctan
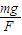 ,斜向右下方或左上方.
,斜向右下方或左上方.(3)由动能定理可知道,△Ek=F合?scosθ,因s一定,F合有最大值时最△Ek最大.
设后来所加的外力F斜向右上方且与水平方向的夹角为θ,则
物体所受的合力为F合=F+Fcosθ-f=0
在竖直方向Fsinθ+N-mg=0
由摩擦定律 f=μN
解得F合=F(cosθ+μsinθ)
令tanα=μ,则
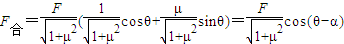
由上式可知当cos(θ-α)=1,α=θ=arctan
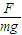 ,
,即所加外力斜向右上方与水平夹角为arctan
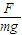 时
时F取最大值Fmax=
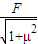
答:1)物体与水平面间的动摩擦因数为
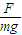 ;
;(2)在物体上再施加另一个大小为F的力,
①若要使物体仍沿原方向做匀速运动,所加外力F与水平面的夹角为arctan
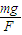 ,斜向右下方或左上方;
,斜向右下方或左上方;②若要使物体沿原方向移动距离s后动能的增加最大,所加外力斜向右上方与水平夹角为arctan
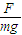 .
.点评:本题主要考查了同学们受力分析的能力,要求同学们能根据平衡条件列式求解,知道s一定时,F合有最大值时最△Ek最大,难度适中.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目