题目内容
 如图所示,在xOy坐标的第一象限内分布有垂直xOy平面向外的匀强磁场,磁感应强度大小为B=2.5×10-2T.在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线垂直y轴),极板间距d=0.4m,极板与左侧电路相连接,通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压U=
如图所示,在xOy坐标的第一象限内分布有垂直xOy平面向外的匀强磁场,磁感应强度大小为B=2.5×10-2T.在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线垂直y轴),极板间距d=0.4m,极板与左侧电路相连接,通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压U=
| ||
| 3 |
| q |
| m |
(1)当滑动头P在a端时,求粒子在磁场中做圆周运动的半径R0;
(2)滑动头P的位置不同则粒子在磁场中运动的时间也不同,求粒子在磁场中运动的最长时间.
分析:(1)当滑动头P在a端时,粒子在磁场中运动的速度大小为v0,根据洛伦兹力提供向心力求出粒子在磁场中做圆周运动的半径.
(2)当粒子射入磁场时速度偏转角越大则粒子在磁场中运动的时间就越长,当滑动头P滑到b端时,偏转电压最大,分析粒子是否打到极板上,若未达到极板上,偏转角最大,粒子在磁场中运动的时间最长,根据偏转角的大小,结合周期公式求出最长的时间.
(2)当粒子射入磁场时速度偏转角越大则粒子在磁场中运动的时间就越长,当滑动头P滑到b端时,偏转电压最大,分析粒子是否打到极板上,若未达到极板上,偏转角最大,粒子在磁场中运动的时间最长,根据偏转角的大小,结合周期公式求出最长的时间.
解答:解:(1)当滑动头P在a端时,粒子在磁场中运动的速度大小为v0,设粒子做圆周运动的半径为R0,有:
qv0B=m
代入数据解得R0=0.2m.
(2)设粒子射出极板时的速度大小为v,偏向角为α,粒子在MN间的运动时间为t0,偏转位移为y,有:
L=v0t0,
y=
?
t02,
v=
,
tanα=
=
,
即y=
Ltanα
设粒子在磁场中做圆周运动的半径为R,由
qvB=m
,得R=
=
.
粒子在磁场中做圆周运动的轨迹如图所示,圆心为O′,与x轴的交点为D,设∠O′DO=β,根据几何关系:
+y=Rcosα+Rsinβ
代入相关数据得,sinβ=sinα,即β=α.
设粒子在磁场中运动的周期为T,则T=
,
粒子在磁场中运动的时间为t=
?T=
.
由此可知,当粒子射入磁场时速度偏转角越大则粒子在磁场中运动的时间就越长,当滑动头P滑到b端时,
UMN=U=
×102V,
代入y=
?
t02=
,
得ym=
m<0.2m.
所以tanαm=
=
=
,
即αm=
.
所以粒子在磁场中运动的最长时间tm=
=
×10-4s.
答:(1)粒子在磁场中做圆周运动的半径为0.2m.
(2)粒子在磁场中运动的最长时间为
×10-4s.

qv0B=m
| v02 |
| R0 |
代入数据解得R0=0.2m.
(2)设粒子射出极板时的速度大小为v,偏向角为α,粒子在MN间的运动时间为t0,偏转位移为y,有:
L=v0t0,
y=
| 1 |
| 2 |
| qUMN |
| md |
v=
| v0 |
| cosα |
tanα=
| vy |
| v0 |
| qUMNt0 |
| mdv0 |
即y=
| 1 |
| 2 |
设粒子在磁场中做圆周运动的半径为R,由
qvB=m
| v2 |
| R |
| mv |
| qB |
| R0 |
| cosα |
粒子在磁场中做圆周运动的轨迹如图所示,圆心为O′,与x轴的交点为D,设∠O′DO=β,根据几何关系:
| d |
| 2 |
代入相关数据得,sinβ=sinα,即β=α.
设粒子在磁场中运动的周期为T,则T=
| 2πm |
| qB |
粒子在磁场中运动的时间为t=
| ||
| 2π |
| m(π+4α) |
| 2qB |
由此可知,当粒子射入磁场时速度偏转角越大则粒子在磁场中运动的时间就越长,当滑动头P滑到b端时,
UMN=U=
| ||
| 3 |
代入y=
| 1 |
| 2 |
| qUMN |
| md |
| qUMNL2 |
| 2mdv02 |
得ym=
| ||
| 15 |
所以tanαm=
| qUt0 |
| mdv0 |
| qUL |
| mdv02 |
| ||
| 3 |
即αm=
| π |
| 6 |
所以粒子在磁场中运动的最长时间tm=
| 5πm |
| 6qB |
| π |
| 12 |
答:(1)粒子在磁场中做圆周运动的半径为0.2m.
(2)粒子在磁场中运动的最长时间为
| π |
| 12 |
点评:本题考查了带电粒子在电场中的偏转和在磁场中做匀速圆周运动,综合性较强,对数学能力的要求较高,需加强训练.

练习册系列答案
相关题目
 如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形,g=10m/s2)
如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形,g=10m/s2) 如图所示,在竖直平面的xoy坐标系中,oy竖直向上,ox水平.该平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿oy方向竖直向上抛出,初速度为V0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形)求:
如图所示,在竖直平面的xoy坐标系中,oy竖直向上,ox水平.该平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿oy方向竖直向上抛出,初速度为V0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形)求: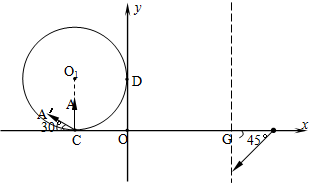 D点进入电场,最后从G点以与x轴正向夹角为45°的方向射出电场.求:
D点进入电场,最后从G点以与x轴正向夹角为45°的方向射出电场.求:
