题目内容
（2011?丰台区二模）如图所示，匀强磁场中有两条水平放置的电阻可忽略的光滑平行金属轨道，轨道左端接一个阻值为R的电阻，R两端与电压传感器相连．一根导体棒（电阻为r）垂直轨道放置，从t=0时刻起对其施加一向右的水平恒力F，使其由静止开始向右运动．用电压传感器瞬时采集电阻R两端的电压U并用计算机绘制出U-t图象．若施加在导体棒上的水平恒力持续作用一段时间后撤去，那么计算机绘制的图象可能是（ ）分析：分析水平恒力作用下导体棒的运动情况，由牛顿第二定律研究导体棒加速度如何变化，由欧姆定律得到电阻R两端的电压U与速度的表达式，再分析U与时间的关系．
解答：解：设导体棒的长度为L，质量为m．施加在导体棒上的水平恒力后，导体棒从静止开始做加速运动，随着速度增大，感应电流增大，导体棒所受的安培力增大，合力减小，加速度减小，由牛顿第二定律得：F-
=ma，则导体棒做加速度减小的变加速运动．电阻R两端的电压U=
E=
BLv，则知，U与速度v成正比，速度增大，U增大，v增大变慢时，U增大也变慢，则U-t图象的斜率变小．
撤去F后，导体棒水平方向只受安培力，导体棒做减速运动，速度减小，安培力减小，加速度减小，速度减小由快变慢，则U减小也由快变慢，U-t图象的斜率逐渐减小．故A正确．
故选A
| B2L2v |
| R+r |
| R |
| R+r |
| R |
| R+r |
撤去F后，导体棒水平方向只受安培力，导体棒做减速运动，速度减小，安培力减小，加速度减小，速度减小由快变慢，则U减小也由快变慢，U-t图象的斜率逐渐减小．故A正确．
故选A
点评：本题根据牛顿第二定律对导体棒的运动过程进行动态分析是关键，要抓住安培力与速度成正比，U与v正比分析图象的斜率变化．
练习册系列答案
相关题目
（2011?丰台区二模）如图所示，竖直平面内有四分之一圆弧轨道固定在水平桌面上，圆心为O点．一小滑块自圆弧轨道A处由静止开始自由滑下，在B点沿水平方向飞出，落到水平地面C点．已知小滑块的质量为m=1.0kg，C点与B点的水平距离为1.0m，B点高度为1.25m，圆弧轨道半径R=1.0m，取g=10m/s2．求小滑块：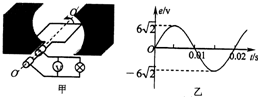
（2011?丰台区二模）如图甲所示为一台小型发电机构造的示意图，线圈逆时针转动，产生的电动势随时间变化的正弦规律图象如图乙所示．发电机线圈电阻为1.0Ω，外接灯泡的电阻为9.0Ω．则（ ）