题目内容
10. 如图所示,为一个均匀透明介质球,球心位于O点,半径为R.一束单色光从真空中沿DC方向平行于直径AOB射到介质球上的C点,DC与AB的距离H=$\frac{\sqrt{3}R}{2}$.若该光束射入球体经一次反射后由E点(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c,则( )
如图所示,为一个均匀透明介质球,球心位于O点,半径为R.一束单色光从真空中沿DC方向平行于直径AOB射到介质球上的C点,DC与AB的距离H=$\frac{\sqrt{3}R}{2}$.若该光束射入球体经一次反射后由E点(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c,则( )| A. | 介质球的折射率为n=3 | |
| B. | 若增大入射光的频率,则该出射光线仍与入射光线平行 | |
| C. | 光束从C点射入到从E点射出所经历的总时间为$\frac{6R}{C}$ | |
| D. | 若介质球的折射率增大,则该出射光线仍与入射光线平行 |
分析 作出光路图,由几何知识求出光线在C点的入射角与折射角,由折射定律n=$\frac{sini}{sinr}$求出折射率.由几何知识求出光从C点射入到从E点射出通过的总路程,由v=$\frac{c}{n}$求出光在球内传播的速度,即可求得时间;根据光路的可逆性分析射入球体内的光线能否发生全反射.若介质球的折射率增大,分析折射角的变化,判断出射光线与入射光线是否平行.
解答  解:A、根据对称性和反射定律、折射定律作出光路如图所示.光线经反射后到达介质与空气的界面时,由几何关系和折射定律得:
解:A、根据对称性和反射定律、折射定律作出光路如图所示.光线经反射后到达介质与空气的界面时,由几何关系和折射定律得:
i′=r,r′=i ①
折射光线PQ与入射光线DC平行,则:∠COA=i
则 sini=$\frac{H}{R}$=$\frac{\sqrt{3}}{2}$,i=60° ②
由图可知i=2r,则得折射角 r=30°
故球的折射率为 n=$\frac{sini}{sinr}$=$\frac{sin60°}{sin30°}$=$\sqrt{3}$.故A错误;
B、若增大入射光的频率,折射率增大,折射角r减小,折射光线射到B点的下方,光路不具有对称性,根据反射定律和折射定律可知,出射光线与入射光线不再平行.故B错误.
C、光从C射入到射出通过的路程是S=4Rcos30°,光在介质中传播速度v=$\frac{c}{n}$,则该光从C射入到从E射出的总时间 t=$\frac{s}{v}$=$\frac{4Rncos30°}{c}$=$\frac{6R}{c}$.故C正确;
D、若介质球的折射率增大,折射角r减小,i′增大,r′也增大,根据几何知识得知出射光线与入射光线不再平行.故D错误.
故选:C.
点评 本题考查对全反射、折射现象的理解与运用能力,作出光路图,根据反射的对称性特点和几何知识求解入射角与折射角是关键.

 原在水平地面上的小物块受到瞬时撞击后,沿光滑斜面向上滑动,如图所示,则小物块沿斜面向上滑动的过程中受到几个力作用( )
原在水平地面上的小物块受到瞬时撞击后,沿光滑斜面向上滑动,如图所示,则小物块沿斜面向上滑动的过程中受到几个力作用( )| A. | 一个 | B. | 两个 | C. | 三个 | D. | 四个 |

(1)根据原理图,连接实验器材,且s断开;
①多用电表选择“x1”挡,先欧姆调零,后用红表笔接a端,黑表笔接b端,记录下R1示数(如图2所示);
③s闭合,多用电表选择“直流电压2.5V”挡,红表笔接a端,黑表笔接b端(填“红”或“黑”),记录下示数U1;然后再测出b、c间的电压,记录下示数U2
④调节滑动变阻器,重复步骤③,得到如下表所示的6组数据;
| U1/V | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| U2/V | 1.05 | 0.90 | 0.75 | 0.70 | 0.45 | 0.30 |
(3)小明在如图3所示的坐标纸中画出了U2-U1关系图;该电池的内电阻为4.0Ω.(保留两位有效数字)
 如图1所示,闭合回路由电阻R与导线组成,其内部磁场大小按B-t图变化(如图2),方向垂直纸面向里,则回路中( )
如图1所示,闭合回路由电阻R与导线组成,其内部磁场大小按B-t图变化(如图2),方向垂直纸面向里,则回路中( )| A. | 电流强度越来越大 | B. | 电流方向为逆时针方向 | ||
| C. | 磁通量的变化率恒定不变 | D. | 产生的感应电动势越来越大 |
| A. | 光波是电磁波 | B. | 干涉现象说明光具有粒子性 | ||
| C. | 光电效应现象说明光具有波动性 | D. | 光的偏振现象说明光是纵波 |
 如图所示,在xoy坐标系中,以(r,0)为圆心、r为半径的圆形区域内存在匀强磁场,磁场区域的圆心为O′,磁场的磁感应强度大小为B,方向垂直于纸面向里.在y>r的足够大的区域内,存在沿y轴负方向的匀强电场,场强大小为E.从O点以相同速率向不同方向发射质子,质子的运动轨迹均在纸面内,且质子在磁场中运动的轨迹半径也为r.已知质子的电荷量为q,质量为m,不计质子所受重与及质子间相互作用力的影响.
如图所示,在xoy坐标系中,以(r,0)为圆心、r为半径的圆形区域内存在匀强磁场,磁场区域的圆心为O′,磁场的磁感应强度大小为B,方向垂直于纸面向里.在y>r的足够大的区域内,存在沿y轴负方向的匀强电场,场强大小为E.从O点以相同速率向不同方向发射质子,质子的运动轨迹均在纸面内,且质子在磁场中运动的轨迹半径也为r.已知质子的电荷量为q,质量为m,不计质子所受重与及质子间相互作用力的影响.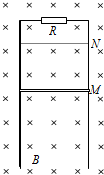 如图所示,在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑的平行金属导轨,导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻.将一根金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.已知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.
如图所示,在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑的平行金属导轨,导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻.将一根金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.已知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g. 如图所示实验装置可实现原子核的人工转变,当装置的容器内通入气体B时,荧光屏上观察到闪光.图中气体B是氮气,该原子核人工转变的核反应方程式是24He+714N→817O+11H.
如图所示实验装置可实现原子核的人工转变,当装置的容器内通入气体B时,荧光屏上观察到闪光.图中气体B是氮气,该原子核人工转变的核反应方程式是24He+714N→817O+11H.