题目内容
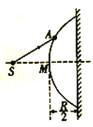
【题目】有一玻璃球冠，右侧面镀银，光源S位于其对称轴上，如图所示.从光源S发出的一细光束射到球面上的A点，其反射光恰好垂直于球冠的对称轴，折射进入玻璃球冠内的光经右侧镀银面第一次反射后恰能沿原路返回.若球面半径为R，球冠高为
，玻璃折射率为
，光在真空中的传播速度为c.求：
（1）光源S与球冠顶点M之间的距离SM；
（2）光在玻璃中的传播时间.
【答案】（1）
，（2）
【解析】
考查折射定律，光的传播。
（1）经右侧镀银面第一次反射恰能沿原路返回，说明折射光垂直于右侧镀银面，其光路如图所示。
设光在A点射入玻璃，入射到右侧镀银面的B点，并按原路返回
由题意可知：
由折射定律得：
解得
，
设球冠的球心为O，对三角形OAS：
所以，三角形OAS为等腰三角形。
光源S与球冠顶点M之间的距离：
（2）
光在玻璃中的传播时间为
解得：
练习册系列答案
相关题目
