Question

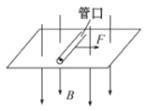
【题目】如图所示，区域AOC内存在垂直纸面向内的匀强磁场，磁感应强度为B，AOC上方有方向竖直向下的匀强电场，∠AOC＝30°，O点右侧L处S点向各个方向发射速度均为v的相同带正电粒子，粒子质量为m，带电量为q，粒子在磁场中运动的最短时间t＝，问：

(1)粒子运动半径r为多少？

(2)粒子在磁场中运动的最长时间是多少？

(3)接第(2)问，粒子进入匀强电场后，能够打在O点，匀强电场场强大小为多少？

Answer 1

【答案】(1) L　(2)　(3)

【解析】

(1)粒子在磁场中运动最短时间:

t＝T＝·＝

得到此时对应的圆心角θ＝π,粒子速度均为v，半径大小均相等，在磁场中运动时间最短时，对应的弦长最短，即到AO边的距离最短，如图所示:

弦垂直于AO边，根据几何关系可得半径

r＝＝L

(2)粒子在磁场中运动最长时间所对应的弦长最长，如图所示:

可知此时粒子从S点射出后从Q点飞出，此时SQ之间距离为

Ltan ∠AOC＝L＝2r

易知粒子运动的最长时间

t′＝＝

(3)进入匀强的电场区域后,粒子做类平抛运动，打在O点时水平位移:

x＝vt″＝L

竖直位移:

y＝L＝at″2,a＝

解得:

E＝