题目内容
18. 如图所示,两条互相平行距离为L=0.5m的光滑金属导轨位于水平桌面内,在导轨的一端接有阻值为R=0.3Ω的电阻,轨道区域内有一磁感应强度B=0.5T的匀强磁场,磁场方向垂直水平桌面竖直向上;有一质量为m1=0.4kg,电阻为r=0.2Ω的金属直杆ab垂直放置在导轨上,直杆中心O′用水平细线栓着,细线通过光滑的滑轮后与质量为m2=0.1kg的P物体连接.不计轨道电阻和接触电阻,g取10m/s2,杆离桌子边缘足够远.求:
如图所示,两条互相平行距离为L=0.5m的光滑金属导轨位于水平桌面内,在导轨的一端接有阻值为R=0.3Ω的电阻,轨道区域内有一磁感应强度B=0.5T的匀强磁场,磁场方向垂直水平桌面竖直向上;有一质量为m1=0.4kg,电阻为r=0.2Ω的金属直杆ab垂直放置在导轨上,直杆中心O′用水平细线栓着,细线通过光滑的滑轮后与质量为m2=0.1kg的P物体连接.不计轨道电阻和接触电阻,g取10m/s2,杆离桌子边缘足够远.求:(1)金属直杆由静止开始运动所能达到的最大速度vm;
(2)当金属杆速度为v=4m/s时,金属杆的加速度a大小.
分析 (1)金属直杆加速度为零,即匀速运动时速度最大,由平衡条件和安培力与速度的关系式结合解答.
(2)先求出金属杆受到的安培力,再由牛顿第二定律求解加速度.
解答 解(1)当金属杆的加速度a=0时速度最大,设最大速度为vm.
对ab杆有:F-BIL=0
根据闭合电路欧姆定律有:
I=$\frac{E}{R+r}$
金属杆切割磁感线产生的感应电动势 E=BLvm;
对物体P有:F=m2g
联立得:vm=$\frac{{m}_{2}g(R+r)}{{B}^{2}{L}^{2}}$=$\frac{0.1×10×(0.3+0.2)}{0.{5}^{2}×0.{5}^{2}}$m/s=8m/s
(2)根据牛顿第二定律:
对金属杆,F-BIL=m1a
对物体P,m2g-F=m2a
联立解得:$a=\frac{{{m_2}g-\frac{{{B^2}{L^2}v}}{(R+r)}}}{{{m_1}+{m_2}}}=1m/{s^2}$
答:(1)金属直杆由静止开始运动所能达到的最大速度vm为8m/s.
(2)当金属杆速度为v=4m/s时,金属杆的加速度a大小为1m/s2.
点评 解决本题的关键要能熟练推导出安培力与速度的关系式,运用力学基本规律,如平衡条件和牛顿第二定律解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.如图甲,手提电脑散热底座一般设置有四 个卡位用来调节角度.某同学将电脑放在散热底座上,为了获得更好的舒适度,由原卡位1调至卡位4(如图乙),电脑始终处于静止状态,则( )


| A. | 电脑受到的支持力变小 | B. | 电脑受到的摩擦力变大 | ||
| C. | 电脑所受的合力变大 | D. | 电脑对底座的作用力不变 |
6.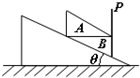 如图所示,倾角为θ=30°的光滑斜面上固定有竖直光滑挡板P,质量相同的横截面为直角三角形的两物块A、B叠放在斜面与档板之间,且A与B间的接触面水平.则A对B的压力与B对斜面的压力之比应为( )
如图所示,倾角为θ=30°的光滑斜面上固定有竖直光滑挡板P,质量相同的横截面为直角三角形的两物块A、B叠放在斜面与档板之间,且A与B间的接触面水平.则A对B的压力与B对斜面的压力之比应为( )
 如图所示,倾角为θ=30°的光滑斜面上固定有竖直光滑挡板P,质量相同的横截面为直角三角形的两物块A、B叠放在斜面与档板之间,且A与B间的接触面水平.则A对B的压力与B对斜面的压力之比应为( )
如图所示,倾角为θ=30°的光滑斜面上固定有竖直光滑挡板P,质量相同的横截面为直角三角形的两物块A、B叠放在斜面与档板之间,且A与B间的接触面水平.则A对B的压力与B对斜面的压力之比应为( )| A. | 2:1 | B. | $\sqrt{3}$:2 | C. | $\sqrt{3}$:1 | D. | $\sqrt{3}$:4 |
8.用100N的力将0.5Kg的足球以8m/s的速度沿水平方向踢出20m,则人对球做的功( )
| A. | 200J | B. | 16J | C. | 2000J | D. | 无法确定 |

 某兴趣小组查阅资料获知,弹簧振子做简谐运动的周期T=2π$\sqrt{\frac{m}{k}}$(其中m是振子的质量,k是弹簧的劲度系数,弹簧质量忽略不计),利用该规律可以测定物体的质量.现有如下器材可供选择:
某兴趣小组查阅资料获知,弹簧振子做简谐运动的周期T=2π$\sqrt{\frac{m}{k}}$(其中m是振子的质量,k是弹簧的劲度系数,弹簧质量忽略不计),利用该规律可以测定物体的质量.现有如下器材可供选择: 一带电量为+Q的正点电荷固定在真空中,形成的电场如图所示,现有一质量为m的带电微粒,在此点电荷附近做匀速圆周运动,周期为T,微粒的重力不能忽略,求
一带电量为+Q的正点电荷固定在真空中,形成的电场如图所示,现有一质量为m的带电微粒,在此点电荷附近做匀速圆周运动,周期为T,微粒的重力不能忽略,求 一定质量的理想气体,其状态变化如图中箭头所示顺序进行,则AB段是等容过程,遵守查理定律;BC段是等压过程,遵守盖•吕萨克定律;若CA段是以纵轴和横轴为渐近线的双曲线的一部分,则CA段是等温过程,遵守玻意耳 定律.
一定质量的理想气体,其状态变化如图中箭头所示顺序进行,则AB段是等容过程,遵守查理定律;BC段是等压过程,遵守盖•吕萨克定律;若CA段是以纵轴和横轴为渐近线的双曲线的一部分,则CA段是等温过程,遵守玻意耳 定律.