题目内容
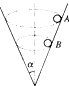 如图所示,在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在各自的水平面内做匀速圆周运动,其中小球A的位置在小球B的上方.下列判断正确的是( )
如图所示,在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在各自的水平面内做匀速圆周运动,其中小球A的位置在小球B的上方.下列判断正确的是( )| A、A球的速率等于B球的速率 | B、A球的角速度大于B球的角速度 | C、A球对漏斗壁的压力等于B球对漏斗壁的压力 | D、A球的转动周期等于B球的转动周期 |
分析:涉及物理量较多时,比较多个量中两个量的关系,必须抓住不变量,而后才能比较变量.
小球受重力和支持力,靠重力和支持力的合力提供圆周运动的向心力,根据F合=ma=m
=mrω2比较线速度、角速度、的大小,根据周期和角速度的关系判断周期大小.
小球受重力和支持力,靠重力和支持力的合力提供圆周运动的向心力,根据F合=ma=m
| v2 |
| r |
解答:解:对A、B两球进行受力分析,两球均只受重力和漏斗给的支持力FN.如图所示
对A球由牛顿第二定律:
FNAsinα=mg----------------------①
FNAcosα=m
=mωA2rA-----------------------②
对B球由牛顿第二定律:
FNBsinα=mg----------------------③
FNBcosα=m
=mωB2rB-------------------------④
由两球质量相等可得FNA=FNB,所以C正确.
由②④可知,两球所受向心力相等.
m
=m
,因为rA>rB,所以vA>vB,故A项错误.
mωA2rA=mωB2rB,因为rA>rB,所以ωA<ωB,故B项错误.
又因为T=
,所以TA>TB,所以D错误.
故选:C.

对A球由牛顿第二定律:
FNAsinα=mg----------------------①
FNAcosα=m
| vA2 |
| rA |
对B球由牛顿第二定律:
FNBsinα=mg----------------------③
FNBcosα=m
| vB2 |
| rB |
由两球质量相等可得FNA=FNB,所以C正确.
由②④可知,两球所受向心力相等.
m
| vA2 |
| rA |
| vB2 |
| rB |
mωA2rA=mωB2rB,因为rA>rB,所以ωA<ωB,故B项错误.
又因为T=
| 2π |
| ω |
故选:C.
点评:对物体进行受力分析,找出其中的相同的量,再利用圆周运动中各物理量的关系式分析比较,能较好的考查学生这部分的基础知识的掌握情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图所示,在光滑的圆锥面内,两个质量不相同的小球P和Q,沿其内表面在不同的水平面内做半径不同的匀速圆周运动,其中球P的轨道半径较大,则 
| A.球P的角速度较小 | B.球P的向心力较小 |
| C.球P的加速度较大 | D.球P的线速度较大 |
 如图所示,在光滑的圆锥面内,两个质量不相同的小球P和Q,沿其内表面在不同的水平面内作半径不同的匀速圆周运动,其中球P的轨道半径较大,则可判定( )
如图所示,在光滑的圆锥面内,两个质量不相同的小球P和Q,沿其内表面在不同的水平面内作半径不同的匀速圆周运动,其中球P的轨道半径较大,则可判定( ) 如图所示,在光滑的圆锥面内,两个质量不相同的小球P和Q,沿其内表面在不同的水平面内做半径不同的匀速圆周运动,其中球P的轨道半径较大,则( )
如图所示,在光滑的圆锥面内,两个质量不相同的小球P和Q,沿其内表面在不同的水平面内做半径不同的匀速圆周运动,其中球P的轨道半径较大,则( )
