题目内容
如图所示，在直角坐标系的第一象限中存在沿y轴负方向的匀强电场，电场强度大小为E，在第四象限中存在着垂直纸面的匀强磁场，一质量为m、带电量为q的粒子（不计重力）在y轴上的A点以平行x轴的初速度v0射人电场区，然后从电场区进入磁场区，又从磁场区进入电场区，并通过x轴上P点和Q点各一次，已知P点坐标为（a，0），Q点坐标为（b，0），求磁感应强度的大小和方向？分析：粒子先进入电场做类平抛运动，运用运动的分解法，根据牛顿第二定律和运动学公式求出粒子刚离开电场时竖直方向的分速度大小，以及速度与水平方向的夹角；
粒子进入磁场后做匀速圆周运动，由洛伦兹力提供向心力，根据几何关系求得轨迹的半径，由牛顿第二定律求出磁感应强度的大小，根据左手定则判断磁场的方向．要分先进P后进Q和先进Q后进P两种情况进行研究．
粒子进入磁场后做匀速圆周运动，由洛伦兹力提供向心力，根据几何关系求得轨迹的半径，由牛顿第二定律求出磁感应强度的大小，根据左手定则判断磁场的方向．要分先进P后进Q和先进Q后进P两种情况进行研究．
解答：
解：若粒子先进P后进Q：在电场中，粒子做类平抛运动，水平方向做匀速直线运动，竖直方向做匀加速直线运动，则有：
a=v0t
vy=a加t=
t
联立得：vy=
．
设粒子离开电场时速度与水平方向的夹角为α，则有：
tanα=
=
粒子进入磁场时的速率为：v=
．
由电场中偏转可知，粒子带正电，根据左手定则判断可知，磁场方向垂直纸面向里．画出粒子的轨迹如图所示．
根据几何知识得：粒子在磁场中的轨迹半径为：r=
又因：qvB=m
得：B=
=
=
?tanα=
?
=
；
同理可得，若粒子先进Q后进P，磁场方向垂直纸面向外．则有：B=
．
答：若先进P后进Q，则磁感应强度大小为B=
，磁场方向垂直纸面向里．若先进Q后进P，磁感应强度大小为B=
，磁场方向垂直纸面向外．
解：若粒子先进P后进Q：在电场中，粒子做类平抛运动，水平方向做匀速直线运动，竖直方向做匀加速直线运动，则有：a=v0t
vy=a加t=
| qE |
| m |
联立得：vy=
| qEa | ||
m
|
设粒子离开电场时速度与水平方向的夹角为α，则有：
tanα=
| vy |
| v0 |
| qEa | ||
m
|
粒子进入磁场时的速率为：v=
| v0 |
| cosα |
由电场中偏转可知，粒子带正电，根据左手定则判断可知，磁场方向垂直纸面向里．画出粒子的轨迹如图所示．
根据几何知识得：粒子在磁场中的轨迹半径为：r=
| ||
| sinα |
又因：qvB=m
| v2 |
| r |
得：B=
| mv |
| qr |
m?
| ||||
q?
|
| 2mv0 |
| q(b-a) |
| 2mv0 |
| q(b-a) |
| qEa | ||
m
|
| 2Ea |
| q(b-a)v0 |
同理可得，若粒子先进Q后进P，磁场方向垂直纸面向外．则有：B=
| 2Eb |
| (b-a)v0 |
答：若先进P后进Q，则磁感应强度大小为B=
| 2Ea |
| (b-a)v0 |
| 2Eb |
| (b-a)v0 |
点评：本题是带电粒子在组合场中运动的类型，要熟练运用运动的分解法处理类平抛运动的问题，正确画出粒子的轨迹，运用几何关系求出磁场中轨迹的半径，要加强这方面的练习，提高解题能力．
练习册系列答案
相关题目
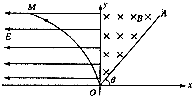如图所示，在直角坐标平面的第I象限内有一匀强磁场区域，磁感应强度为B，直线OA是磁场右侧的边界．在第Ⅱ象限区域，存在电场强度大小为E的水平向左的匀强电场，y轴是电场、磁场区域的分界线曲线，OM满足方程x=-ky2（k＞0）．有一带电荷量为q、质量为m的负粒子（重力不计）在曲线OM上某一点由静止释放，穿越y轴进入磁场中．
（2013?怀化二模）如图所示，在直角坐标xOy平面y轴左侧（含y轴）有一沿y轴负向的匀强电场，一质量为m，电量为q的带正电粒子从x轴上P处以速度ν0沿x轴正向进入电场，从y轴上Q点离开电场时速度变为2ν0，Q点坐标为（0，-d），在y轴右侧有一与坐标平面垂直的矩形匀强磁场区域（图中未画出，粒子过Q点继续运动一段距离后才进入磁场区域），磁场磁感应强度大小
如图所示，在直角坐标xOy平面y轴左侧（含y轴）有一沿y轴负向的匀强电场，一质量为m，电量为q的带正电粒子从x轴上P处以速度v0沿x轴正向进入电场，从y轴上Q点离开电场时速度方向与y轴负向夹角θ=30°，Q点坐标为（0，-d），在y轴右侧有一与坐标平面垂直的有界匀强磁场区域（图中未画出），磁场磁感应强度大小B=
如图所示，在直角坐标xoy的第一象限中分布着指向－y轴方向的匀强电场，在第四象限中分布着垂直纸面向里方向的匀强磁场，一个质量为m、带电＋q的粒子(不计重力)在A点(0，3)以初速V0＝120m/s平行x轴射入电场区域，然后从电场区域进入磁场，又从磁场进入电场，并且只通过x轴上的P点(6，0)和Q点(8，0)各一次，已知该粒子的荷质比为q/m＝108c/kg．
沿x轴正向进入电场，从y轴上Q点离开电场时速度方向与y轴负向夹角
，Q点坐标为（0，-d），在y轴右侧有一与坐标平面垂直的有界匀强磁场区域（图中未画出），磁场磁感应强度大小
，粒子能从坐标原点O沿x轴负向再进入电场．不计粒子重力，求：