题目内容
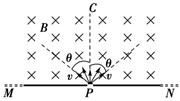
如图所示,在屏MN的上方有磁感应强度为B的匀强磁场,磁场方向垂直于纸面向里.P为屏上的一个小孔.PC与MN垂直.一群质量为m、带电荷量为-q的粒子(不计重力),以相同的速率v,从P处沿垂直于磁场的方向射入磁场区域.粒子入射方向在与磁场B垂直的平面内,且散开在与PC夹角为θ的范围内,则在屏MN上被粒子打中的区域的长度为( )
A. B.
B.
C.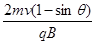 D.
D.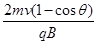
【答案】
D
【解析】
试题分析:任取一粒子分析,作出圆周运动的轨迹,则可得出粒子打在屏上的位置与粒子与PC夹角的关系,则可得出粒子打在屏上的最远点及最近点,即可得出打中的长度.
由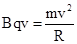 可知:
可知: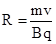
如图所示,
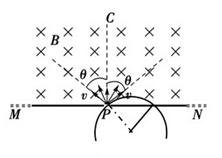
取一粒子,设粒子与PC夹角为α,则由几何关系可知,打在屏上的距离与P点相距
L=2Rcosα
故可知,当α=0时,打在屏上的距离最远,最远距离为2R;当α=θ时,打在屏上的距离最近,最近距离为L′=2Rcosθ;
故有粒子打中的区域为 ;
;
故选D.
考点:带电粒子在匀强磁场中的运动.
点评:带电粒子在磁场运动区域的判断时,要注意寻找一般表达式,通过分析再找出可能的边界;另外本题中关于PC两边对称的粒子方向均可适合L=2Rcosα.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
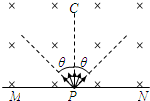 如图所示,在屏MN的上方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里.P为屏上的一小孔.PC与MN垂直.一群质量为m、带电量为-q的粒子(不计重力),以相同的速率v,从P处沿垂直于磁场的方向射入磁场区域.粒子入射方向在与磁场B垂直的平面内,且散开在与PC夹角为θ的范围内.则在屏MN上被粒子打中的区域的长度为( )
如图所示,在屏MN的上方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里.P为屏上的一小孔.PC与MN垂直.一群质量为m、带电量为-q的粒子(不计重力),以相同的速率v,从P处沿垂直于磁场的方向射入磁场区域.粒子入射方向在与磁场B垂直的平面内,且散开在与PC夹角为θ的范围内.则在屏MN上被粒子打中的区域的长度为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,在屏MN的右方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里.P为屏上的一小孔,PC与MN垂直.一群质量为m、带电荷量为-q的粒子(不计重力),以相同的速率v从P处沿垂直于磁场的方向射入磁场区域.粒子入射方向在与磁场B垂直的平面内,且散开在与PC夹角为θ的范围内,则在屏MN上被粒子打中的区域的长度为( )
如图所示,在屏MN的右方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里.P为屏上的一小孔,PC与MN垂直.一群质量为m、带电荷量为-q的粒子(不计重力),以相同的速率v从P处沿垂直于磁场的方向射入磁场区域.粒子入射方向在与磁场B垂直的平面内,且散开在与PC夹角为θ的范围内,则在屏MN上被粒子打中的区域的长度为( )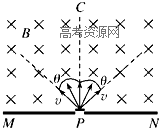 如图所示,在屏MN的上方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里.P为屏上的一小孔,PC与MN垂直.一群质量为m?带电荷量为-q的粒子(不计重力),以相同的速率v,从P处沿垂直于磁场的方向射入磁场区域.粒子入射方向在与磁场B垂直的平面内,且散开在与PC夹角为θ的范围内.求在屏MN上被粒子打中的区域的长度为多少?
如图所示,在屏MN的上方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里.P为屏上的一小孔,PC与MN垂直.一群质量为m?带电荷量为-q的粒子(不计重力),以相同的速率v,从P处沿垂直于磁场的方向射入磁场区域.粒子入射方向在与磁场B垂直的平面内,且散开在与PC夹角为θ的范围内.求在屏MN上被粒子打中的区域的长度为多少?

 B.
B. C.
C. D.
D.