题目内容
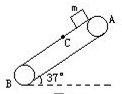 (2005?闵行区二模)如图,传送带与地面倾角θ=37°,逆时针转动,并以v0=10m/s的速度运行着,在传送带上端A处轻轻放一质量m=0.5kg的物体,C处是物块速度等于皮带速度这一瞬间.它与传送带之间的动摩擦因数μ=0.5,AB间长度L=16m,则把物体送到B点时的速度是多少?某学生审完题后用动能定理列出下式:
(2005?闵行区二模)如图,传送带与地面倾角θ=37°,逆时针转动,并以v0=10m/s的速度运行着,在传送带上端A处轻轻放一质量m=0.5kg的物体,C处是物块速度等于皮带速度这一瞬间.它与传送带之间的动摩擦因数μ=0.5,AB间长度L=16m,则把物体送到B点时的速度是多少?某学生审完题后用动能定理列出下式:limgsinθ-Lμmgcosθ=
| 1 |
| 2 |
| 1 |
| 2 |
VB=[2Lg(sinθ-μcosθ)]1/2=…
上述结果是否正确?若正确,列式证明;若错误,求出正确结果.均要有文字说明.(sin37°=0.6 cos37°=0.8)
分析:物体放在传送带上后,开始阶段,传送带的速度大于物体的速度,传送带给物体一沿斜面向下的滑动摩擦力,物体由静止开始加速下滑,当物体加速至与传送带速度相等时,由于μ<tanθ,物体在重力作用下将继续加速,此后物体的速度大于传送带的速度,传送带给物体沿传送带向上的滑动摩擦力,但合力沿传送带向下,物体继续加速下滑,综上可知,滑动摩擦力的方向在获得共同速度的瞬间发生了“突变”.
解答:解:该同学结论错误.由于初始皮带速度大于物块速度,物块相对皮带向上,故皮带对物块的摩擦力沿斜面向下,摩擦力做正功,物块动能增大.当物块速度等于皮带速度这一瞬间,物块相对皮带速度为零,瞬时摩擦力也为零,但由于物块将要继续加速,所以皮带给物块的摩擦力方向为沿斜面向上,一直到物块运动到B端.
正确解法:设物块到达C点的速度vC与皮带速度相等,AC间的距离为s1,则由动能定理得
(mgsinθ+μmgcosθ)s1=
mvC2-
mvA2 ①
(mgsinθ-μmgcosθ)(L-s1)=
mvB2-
mvC2 ②
由①式得:
s1=
=5m
①+②式得:
Lmgsinθ+(2s1-L)μmgcosθ=
mvB2
解得:vB=
=12m/s
答:上述结果是错误的,把物体送到B点时的速度是12m/s.
正确解法:设物块到达C点的速度vC与皮带速度相等,AC间的距离为s1,则由动能定理得
(mgsinθ+μmgcosθ)s1=
| 1 |
| 2 |
| 1 |
| 2 |
(mgsinθ-μmgcosθ)(L-s1)=
| 1 |
| 2 |
| 1 |
| 2 |
由①式得:
s1=
| vC2-vA2 |
| 2g(sinθ+μcosθ) |
①+②式得:
Lmgsinθ+(2s1-L)μmgcosθ=
| 1 |
| 2 |
解得:vB=
| 2g[(Lsinθ+2s1-L)μcosθ] |
答:上述结果是错误的,把物体送到B点时的速度是12m/s.
点评:从上述例题可以总结出,皮带传送物体所受摩擦力可能发生突变,不论是其大小的突变,还是其方向的突变,都发生在物体的速度与传送带速度相等的时刻.

练习册系列答案
相关题目
 (2005?闵行区二模)在水平线上有17个质点,每相邻两质点间的水平距离均为4cm,如图所示.有一简谐波在水平方向传播,已知第5个质点完成一次全振动经过的路程是 8cm,时间为2S.当它从平衡位置开始向上振动经过12cm路程时,第17个质点即将振动,则该波的传播速度是
(2005?闵行区二模)在水平线上有17个质点,每相邻两质点间的水平距离均为4cm,如图所示.有一简谐波在水平方向传播,已知第5个质点完成一次全振动经过的路程是 8cm,时间为2S.当它从平衡位置开始向上振动经过12cm路程时,第17个质点即将振动,则该波的传播速度是 (2005?闵行区二模)倾角为θ≤30°的斜面上,O处的轴上安一个可以自由转动的光滑挡板(如图),当挡板与斜面夹角缓慢增大的过程中光滑斜面对球的支持力和球对挡板的作用力如何变化?( )
(2005?闵行区二模)倾角为θ≤30°的斜面上,O处的轴上安一个可以自由转动的光滑挡板(如图),当挡板与斜面夹角缓慢增大的过程中光滑斜面对球的支持力和球对挡板的作用力如何变化?( ) (2005?闵行区二模)(均做)在“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
(2005?闵行区二模)(均做)在“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图. (2005?闵行区二模)本题中A.B分别为一期教材、二期新教材分叉题,考生选择只能选A组的全部或B组的全部完成
(2005?闵行区二模)本题中A.B分别为一期教材、二期新教材分叉题,考生选择只能选A组的全部或B组的全部完成