题目内容
如图所示,把小球A从地面以10m/s的初速度竖直上抛,同时在球A的正上方离地高为15m的平台上,以5m/s的初速度竖直下抛小球B,若取g=10m/s2,且忽略空气阻力,求:(1)两球在空中相遇的时刻;
(2)相遇点的位置是怎样的;
(3)两球在空中相遇时,速率各是多大.

【答案】分析:(1)球A竖直上抛,球B竖直下抛,根据位移时间关系公式列式求解即可.
(2)根据位移时间关系公式求解相遇点的高度;
(3)根据速度时间关系公式求解A、B球的速率.
解答:解:(1)把每个球的运动分别看成自由落体运动和匀速直线运动的合成.
当研究A球相对B球的相对运动时,它们各自的自由落体分运动部分相互抵消.
在B球看来,A球只做速率为v的匀速直线运动
即:v=10m/s+5m/s=15m/s
两球从抛出到相遇的时间:
t= =
= =1s
=1s
(2)两球相遇地点离地面高度:
h=vOAt- gt2=10×1-
gt2=10×1- ×10×12=5m
×10×12=5m
(3)vtB=vOB+gt=5+10×1=15m/s
vtA=vOA-gt=10-10×1=0m/s
即:A、B两球相遇时速率分别是0 m/s和15 m/s.
答:(1)两球在空中相遇的时刻为1s;
(2)相遇点的离抛出点高度为5m;
(3)两球在空中相遇时,A、B两球速率分别是0 m/s、15 m/s.
点评:本题关键是明确两个小球的运动性质,然后根据运动学公式列式求解,方法多样,可以灵活选择.
(2)根据位移时间关系公式求解相遇点的高度;
(3)根据速度时间关系公式求解A、B球的速率.
解答:解:(1)把每个球的运动分别看成自由落体运动和匀速直线运动的合成.
当研究A球相对B球的相对运动时,它们各自的自由落体分运动部分相互抵消.
在B球看来,A球只做速率为v的匀速直线运动
即:v=10m/s+5m/s=15m/s
两球从抛出到相遇的时间:
t=
 =
= =1s
=1s(2)两球相遇地点离地面高度:
h=vOAt-
 gt2=10×1-
gt2=10×1- ×10×12=5m
×10×12=5m(3)vtB=vOB+gt=5+10×1=15m/s
vtA=vOA-gt=10-10×1=0m/s
即:A、B两球相遇时速率分别是0 m/s和15 m/s.
答:(1)两球在空中相遇的时刻为1s;
(2)相遇点的离抛出点高度为5m;
(3)两球在空中相遇时,A、B两球速率分别是0 m/s、15 m/s.
点评:本题关键是明确两个小球的运动性质,然后根据运动学公式列式求解,方法多样,可以灵活选择.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
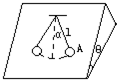 用长为L的细线把一个小球悬挂在倾角为θ的光滑斜面上,然后将小球偏离自然悬挂的位置拉到A点,偏角α≤5°,如图所示.当小球从A点无初速释放后,小球在斜面上往返振动的周期为( )
用长为L的细线把一个小球悬挂在倾角为θ的光滑斜面上,然后将小球偏离自然悬挂的位置拉到A点,偏角α≤5°,如图所示.当小球从A点无初速释放后,小球在斜面上往返振动的周期为( )A、2π
| ||||
B、2π
| ||||
C、2π
| ||||
D、2π
|
 质量为m的小球,用长为l的细线悬挂在O点,在O点的正下方
质量为m的小球,用长为l的细线悬挂在O点,在O点的正下方 如图所示,把小球A从地面以10m/s的初速度竖直上抛,同时在球A的正上方离地高为15m的平台上,以5m/s的初速度竖直下抛小球B,若取g=10m/s2,且忽略空气阻力,求:
如图所示,把小球A从地面以10m/s的初速度竖直上抛,同时在球A的正上方离地高为15m的平台上,以5m/s的初速度竖直下抛小球B,若取g=10m/s2,且忽略空气阻力,求: