题目内容
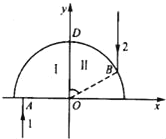
【题目】由不同介质制成的两个半径均为R的透明四分之一圆柱体I和Ⅱ紧靠在一起，截面如图所示，圆心为O，顶部交点为D，以O为原点建立直角坐标系xOy．红色光束1从介质I底部的A（
，0）点垂直于界面入射；红色光束2平行于y轴向下射入介质Ⅱ，入射点为B且∠BOD=60°．已知透明介质I对红光的折射率n1=
，透明介质Ⅱ对红光的折射率n2=
．设光束1经柱体I的圆弧面后与y轴交点为P,光束2经柱体Ⅱ的下底面后与y轴交点为Q ．求：P、Q两交点的距离。
【答案】
【解析】
红光线1对介质 I的全反射临界角为：
，而光线1由A点入射后的入射角i1=60°＞45°，所以将会发生全反射，根据几何关系可知：反射后恰好交y轴于D点，设红光线2在B点发生的折射的折射角为r2，由折射定律
得：
，所以：r2=30°，根据几何关系光线2再传播到底部介面时入射角 i3=30°，光线2对介质 II的全反射临界角为：
，所以不会发生全反射，再由折射定律得折射角：r3=60°，设光线2射出后交y轴于P点，依据几何关系：
，所以所求的距离 d=DP=R+
R=
R
练习册系列答案
相关题目
