题目内容
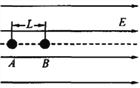
【题目】如图所示，将截面为正方形的真空腔abcd放置在一匀强磁场中，磁场方向垂直纸面向里．若有一束具有不同速率的电子由小孔a沿ab方向射入磁场，打在腔壁上被吸收，则由小孔c和d射出的电子的速率之比；通过磁场的时间之比为 ． 
【答案】2：1；1：2
【解析】解：①设电子的质量为m，电量为q，磁感应强度为B，电子圆周运动的半径为r，速率为v，由牛顿第二定律得：evB=m 
，
解得：v= 
，r与v成正比．
由图看出，从c孔和d孔射出的电子半径之比rc：rd=2：1，则速率之比vc：vd=rc：rd=2：1．
②电子圆周运动的周期为：T= 
，所有电子的周期相等，
从c孔和d孔射出的电子在盒内运动时间分别为：tc= 
T，td= 
，
所以从c孔和d孔射出的电子在盒内运动时间之比：tc：td=1：2；
所以答案是：2：1，1：2．
【考点精析】掌握洛伦兹力和感应电流的方向是解答本题的根本，需要知道洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功；通电导体在磁场中受力方向：跟电流方向和磁感线方向有关．（左手定则）．
练习册系列答案
相关题目
