Question

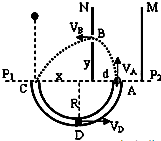
如图所示，p₁，p₂为一水平面，其上方紧贴放置一对竖直正对的带电金属板M、N，其下方紧贴放置一内壁光滑的绝缘轨道ADC，绝缘轨道ADC位于竖直平面内，右端A恰在两板的正中央处，N板上开有小孔B，孔B到水面P₁，P₂的距离为绝缘轨道直径的倍．设仅在M、N两板之间存在匀强电场．现在左端C的正上方某一位置，将一质量为m、电荷量为q的小球静止释放，经过绝缘轨道CDA后从A端竖直向上射入两板间，小球能从B孔水平射出，并恰好落到c端．整个过程中，小球的电荷量不变，孔B的大小及小球的直径均可忽略，重力加速度为g．求：
（1）板间电场强度E；
（2）小球运动到绝缘轨道最低点D时对轨道的压力大小．

Answer 1

【答案】分析：分析物体的运动过程与受力情况，可知物体先在重力与电场力的作用下做类平抛运动，再做圆周运动，然后再做类平抛运动；由类平抛运动的规律可求得场强大小；在从D到A的过程中物体机械能守恒；由机械能守恒可求得D点的速度，再由向心力公式可求得D点的压力．
解答：解：（1）如图，设绝缘轨道半径为R，A到板N距离为d，AB的竖直距离为y，C到板N的距离为x；到达最低点D的速度为v_D，到A点的速度为v_A，到达孔B时的速度为v_B．
球在离开A经B到C的过程中，竖直方向小球受重力作用，故从A到B和从B到C的时间相等，并设从A到B的时间为t．
则有：d=t
x=v_Bt
联立解得：x=2d
由题意可得，y=（x+d）
在水平方向上，有d=t²
在竖直方向上，有：y=gt²
解得板间场强大小为：E=；
（2）从A到B的过程中，有v_A²=2gy
由题意可得x+d=2R
联立解得v_A²=Rg
从D到A，根据机械能守恒，有mv_D²=mgR+mv_A²
在D点，有：F-mg=m
解得F=mg；
答：（1）板间场强为；（2）小球运动到绝缘轨道最低点D时对轨道的压力为mg．

点评：本题小球处于电场和重力场中，平抛运动中小球的运动由运动的合成与分解规律进行求解；而圆周运动中注意分析向心力及应用机械能守恒定律求解．