题目内容
如图所示,两根足够长的平行金属导轨由倾斜和水平两部分平滑连接组成,导轨间距L=1m,倾角θ=45°,水平部分处于磁感应强度B=1T的匀强磁场中,磁场方向竖直向上,磁场左边界MN与导轨垂直.金属棒ab质量m1=0.2kg,电阻R1=1Ω,金属棒cd质量m2=0.2kg,电阻R2=3Ω,导轨电阻不计,两棒与导轨间动摩擦因数μ=0.2.开始时,棒ab放在斜导轨上,与水平导轨高度差h=1m,棒cd放在水平轨上,距MN距离为s0.两棒均与导轨垂直,现将ab棒由静止释放,取g=10m/s2.求:

(1)棒ab运动到MN处的速度大小;
(2)棒cd运动的最大加速度;
(3)若导轨水平部分光滑,要使两棒不相碰,棒cd距离MN的最小距离s0.

(1)棒ab运动到MN处的速度大小;
(2)棒cd运动的最大加速度;
(3)若导轨水平部分光滑,要使两棒不相碰,棒cd距离MN的最小距离s0.
分析:(1)金属棒下降的过程中,重力与摩擦力做功的和等于动能的增加.
(2)运用法拉第电磁感应定律求出感应电动势,求出安培力,再使用牛顿第二定律求出加速度;
(3)运用动量守恒定律求出棒cd距离MN的最小距离时它们的共同速度,运用动量定理求出速度的变化量.根据能量守恒定律,求出产生的焦耳热.
(2)运用法拉第电磁感应定律求出感应电动势,求出安培力,再使用牛顿第二定律求出加速度;
(3)运用动量守恒定律求出棒cd距离MN的最小距离时它们的共同速度,运用动量定理求出速度的变化量.根据能量守恒定律,求出产生的焦耳热.
解答:解:(1)对ab运用动能定理得
m1gh-μm1gcos45°?
=
m1
代人数据得:v0=
=
m/s=4m/s
(2)棒ab运动到MN处,cd加速度最大
Em=BLv0
Im=
∴Fm=BImL=
=
N=1N
由牛顿第二定律:Fm-μm2g=m2a
解得:a=3m/s2
(3)在不相碰的情况下,两棒最终速度必相等,设为vm,ab、cd组成的系统在水平方向任一时刻ab棒与cd棒受到的安培力总是大小相等,方向相反,故系统的水平方向的动量守恒,得:
mv0=2mvm
即:vm=
=2m/s
设某时刻ab的速度为v1,cd的速度为v2,在极小的△t内,ab速度变化为△v
则:ΦE=
=BL(v1-v2)
I=
由牛顿运动定律有F1=m1
=
得v1-v2=
?
两棒在水平导轨运动的相对位移,即为两棒不相碰的最小距离,
S0=∑(v1-v2)△t=
∑△v=
?(v0-
v0)=
联立以上各公式,代人数据求得:s0=1.6m
答:(1)棒ab运动到MN处的速度大小是4m/s;
(2)棒cd运动的最大加速度3m/s2;
(3)棒cd距离MN的最小距离是1.6m
m1gh-μm1gcos45°?
| h |
| sin45° |
| 1 |
| 2 |
| v | 2 0 |
代人数据得:v0=
| 2gh-2μgh |
| 2×10×1-2×0.2×10×1 |
(2)棒ab运动到MN处,cd加速度最大
Em=BLv0
Im=
| Em |
| R1+R2 |
∴Fm=BImL=
| B2L2v0 |
| R1+R2 |
| 12×12×4 |
| 1+3 |
由牛顿第二定律:Fm-μm2g=m2a
解得:a=3m/s2
(3)在不相碰的情况下,两棒最终速度必相等,设为vm,ab、cd组成的系统在水平方向任一时刻ab棒与cd棒受到的安培力总是大小相等,方向相反,故系统的水平方向的动量守恒,得:
mv0=2mvm
即:vm=
| v0 |
| 2 |
设某时刻ab的速度为v1,cd的速度为v2,在极小的△t内,ab速度变化为△v
则:ΦE=
| △Φ |
| △t |
I=
| E |
| R1+R2 |
由牛顿运动定律有F1=m1
| △v |
| △t |
| B2L2(v1-v2) |
| R1+R2 |
得v1-v2=
| (R1+R2)m1 |
| B2L2 |
| △v |
| △t |
两棒在水平导轨运动的相对位移,即为两棒不相碰的最小距离,
S0=∑(v1-v2)△t=
| (R1+R2)m1 |
| B2L2 |
| (R1+R2)m1 |
| B2L2 |
| 1 |
| 2 |
| (R1+R2)m1v0 |
| 2B2L2 |
联立以上各公式,代人数据求得:s0=1.6m
答:(1)棒ab运动到MN处的速度大小是4m/s;
(2)棒cd运动的最大加速度3m/s2;
(3)棒cd距离MN的最小距离是1.6m
点评:该题考查了多个知识点的综合运用.做这类问题我们还是应该从运动过程和受力分析入手研究,运用一些物理规律求解问题.
能量的转化与守恒的应用非常广泛,我们应该首先考虑.
能量的转化与守恒的应用非常广泛,我们应该首先考虑.

练习册系列答案
相关题目
 如图所示,两根足够长的光滑金属导轨MN、PQ平行放置,导轨平面与水平面的夹角为θ,导轨的下端接有电阻.当导轨所在空间没有磁场时,使导体棒ab以平行导轨平面的初速度v0冲上导轨平面,ab上升的最大高度为H;当导轨所在空间存在方向与导轨平面垂直的匀强磁场时,再次使ab以相同的初速度从同一位置冲上导轨平面,ab上升的最大高度为h.两次运动中导体棒ab始终与两导轨垂直且接触良好.关于上述情景,下列说法中正确的是( )
如图所示,两根足够长的光滑金属导轨MN、PQ平行放置,导轨平面与水平面的夹角为θ,导轨的下端接有电阻.当导轨所在空间没有磁场时,使导体棒ab以平行导轨平面的初速度v0冲上导轨平面,ab上升的最大高度为H;当导轨所在空间存在方向与导轨平面垂直的匀强磁场时,再次使ab以相同的初速度从同一位置冲上导轨平面,ab上升的最大高度为h.两次运动中导体棒ab始终与两导轨垂直且接触良好.关于上述情景,下列说法中正确的是( )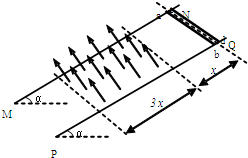 如图所示,两根足够长的平行光滑金属导轨MN、PQ与水平面的夹角为α=30°,导轨电阻不计,导轨处在垂直导轨平面斜向上的有界匀强磁场中.两根电阻都为R=2Ω、质量都为m=0.2kg的完全相同的细金属棒ab和cd垂直导轨并排靠紧的放置在导轨上,与磁场上边界距离为x=1.6m,有界匀强磁场宽度为3x=4.8m.先将金属棒ab由静止释放,金属棒ab刚进入磁场就恰好做匀速运动,此时立即由静止释放金属棒cd,金属棒cd在出磁场前已做匀速运动.两金属棒在下滑过程中与导轨接触始终良好(取重力加速度g=10m/s2).求:
如图所示,两根足够长的平行光滑金属导轨MN、PQ与水平面的夹角为α=30°,导轨电阻不计,导轨处在垂直导轨平面斜向上的有界匀强磁场中.两根电阻都为R=2Ω、质量都为m=0.2kg的完全相同的细金属棒ab和cd垂直导轨并排靠紧的放置在导轨上,与磁场上边界距离为x=1.6m,有界匀强磁场宽度为3x=4.8m.先将金属棒ab由静止释放,金属棒ab刚进入磁场就恰好做匀速运动,此时立即由静止释放金属棒cd,金属棒cd在出磁场前已做匀速运动.两金属棒在下滑过程中与导轨接触始终良好(取重力加速度g=10m/s2).求: 如图所示,两根足够长的固定平行金属导轨位于同一水平面内,导轨间的距离为L,导轨上横放着两根导体棒ab和cd.设两根导体棒的质量皆为m,电阻皆为R,导轨光滑且电阻不计,在整个导轨平面内都有竖直向上的匀强磁场,磁感强度为B.开始时ab和cd两导体棒有方向相反的水平初速,初速大小分别为v0和2v0,求:
如图所示,两根足够长的固定平行金属导轨位于同一水平面内,导轨间的距离为L,导轨上横放着两根导体棒ab和cd.设两根导体棒的质量皆为m,电阻皆为R,导轨光滑且电阻不计,在整个导轨平面内都有竖直向上的匀强磁场,磁感强度为B.开始时ab和cd两导体棒有方向相反的水平初速,初速大小分别为v0和2v0,求: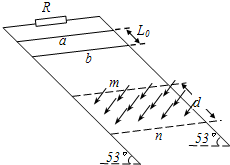 如图所示,两根足够长且平行的光滑金属导轨与水平面成53°夹角固定放置,导轨间连接一阻值为6Ω的电阻R,导轨电阻忽略不计.在两平行虚线m、n间有一与导轨所在平面垂直、磁感应强度为B的匀强磁场.导体棒a的质量为ma=0.4kg,电阻Ra=3Ω;导体棒b的质量为mb=0.1kg,电阻Rb=6Ω;它们分别垂直导轨放置并始终与导轨接触良好.a、b从开始相距L0=0.5m处同时将它们由静止开始释放,运动过程中它们都能匀速穿过磁场区域,当b刚穿出磁场时,a正好进入磁场(g取10m/s2,不计a、b之间电流的相互作用).求:
如图所示,两根足够长且平行的光滑金属导轨与水平面成53°夹角固定放置,导轨间连接一阻值为6Ω的电阻R,导轨电阻忽略不计.在两平行虚线m、n间有一与导轨所在平面垂直、磁感应强度为B的匀强磁场.导体棒a的质量为ma=0.4kg,电阻Ra=3Ω;导体棒b的质量为mb=0.1kg,电阻Rb=6Ω;它们分别垂直导轨放置并始终与导轨接触良好.a、b从开始相距L0=0.5m处同时将它们由静止开始释放,运动过程中它们都能匀速穿过磁场区域,当b刚穿出磁场时,a正好进入磁场(g取10m/s2,不计a、b之间电流的相互作用).求: (2011?湖南模拟)如图所示,两根足够长的光滑平行金属导轨相距为l=0.5m,导轨平面与水平面间的夹角θ=30°,整个导轨平面处于匀强磁场中,磁场的磁感应强度大小B=0.4T,方向垂直导轨平面,在导轨上垂直导轨放置两金属棒ab和cd,长度均为0 5m,cd棒的质量m=0.2kg、电阻R=0.2Ω,不计ab棒和金属导轨的电阻,两棒与金属导轨接触良好且可沿导轨自由滑动.现ab棒在外力作用下,始终以恒定速度v=1.5m/s沿着导轨向上滑动,cd棒则由静止释放,g取10m/s2.求:
(2011?湖南模拟)如图所示,两根足够长的光滑平行金属导轨相距为l=0.5m,导轨平面与水平面间的夹角θ=30°,整个导轨平面处于匀强磁场中,磁场的磁感应强度大小B=0.4T,方向垂直导轨平面,在导轨上垂直导轨放置两金属棒ab和cd,长度均为0 5m,cd棒的质量m=0.2kg、电阻R=0.2Ω,不计ab棒和金属导轨的电阻,两棒与金属导轨接触良好且可沿导轨自由滑动.现ab棒在外力作用下,始终以恒定速度v=1.5m/s沿着导轨向上滑动,cd棒则由静止释放,g取10m/s2.求: