题目内容
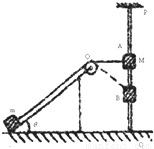
 如图所示,物块M和m用一不可伸长的细绳通过定滑轮连接,m放在倾角θ=37°的固定光滑斜面上,而穿过竖直杆PQ的物块M可沿杆无摩擦地下滑,M=3m,开始时,将M抬高到A点,使细绳水平,此时OA段绳长为L=4.0m,现M由静止开始下滑,求:当M下滑3.0m至B点时的速度为多大?(g取10m/s2)
如图所示,物块M和m用一不可伸长的细绳通过定滑轮连接,m放在倾角θ=37°的固定光滑斜面上,而穿过竖直杆PQ的物块M可沿杆无摩擦地下滑,M=3m,开始时,将M抬高到A点,使细绳水平,此时OA段绳长为L=4.0m,现M由静止开始下滑,求:当M下滑3.0m至B点时的速度为多大?(g取10m/s2)分析:本题的关键是:(1)M和m组成的系统机械能守恒,而M或m的机械能不守恒,(2)物体m上滑的位移为绳长OB与OA之差.
解答:解:物体m上升过程中,不只是重力做功,绳子拉力做正功,所以物体m的机械能不守恒,根据功能关系“除重力以外其它力做的功等于物体机械能的变化”可知物体m的机械能增加,且增加的机械能等于绳子拉力对物体m做的功.
由于两个物体组成的系统在运动过程中只有重力做功,系统机械能守恒,
设M到B点时速度v1,m的速度为v2,
则有:
Mgh-mg(OB-OA)sinθ=
M
+
m
…①
由图可知OB=
=5m,
所以sin∠AOB=
=0.6,即∠AOB=37°,再根据速度的分解,把v1沿OB方向分解,
有v2=v1sin37°…②
联立①②并代入数据解得 v1=7.1m/s.
答:M下滑至B点时的速度为7.1m/s.
由于两个物体组成的系统在运动过程中只有重力做功,系统机械能守恒,
设M到B点时速度v1,m的速度为v2,
则有:
Mgh-mg(OB-OA)sinθ=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
由图可知OB=
| OA2+AB2 |
所以sin∠AOB=
| AB |
| OB |
有v2=v1sin37°…②
联立①②并代入数据解得 v1=7.1m/s.
答:M下滑至B点时的速度为7.1m/s.
点评:遇到相互作用的系统问题,若没有摩擦阻力应用系统机械能守恒定律求解;对“牵连速度”问题,应记住“实际的速度是合速度”和“沿绳子方向的速度相等”的结论.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

 =300的固定的光滑斜面上,而穿过竖直杆PQ的物块M可沿杆无摩擦地下滑,M=3m,开始时将M抬高到A点,使细绳水平,此时OA段的绳长为L=4.0m,现使M由静止开始下滑,则当M下滑3.0m至B点时的速度为(
)(g=10m/s2)
=300的固定的光滑斜面上,而穿过竖直杆PQ的物块M可沿杆无摩擦地下滑,M=3m,开始时将M抬高到A点,使细绳水平,此时OA段的绳长为L=4.0m,现使M由静止开始下滑,则当M下滑3.0m至B点时的速度为(
)(g=10m/s2)